

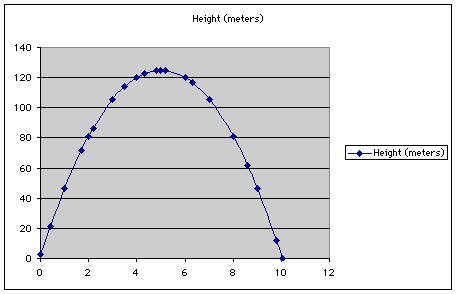
When we connect the data points in Unit 1 by a smooth curve, we get a shape called a parabola. The figure below is the graph of the data from Unit 1.
Here are several other graphs of parabolas:
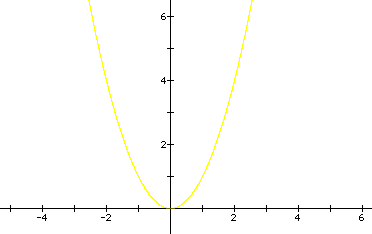
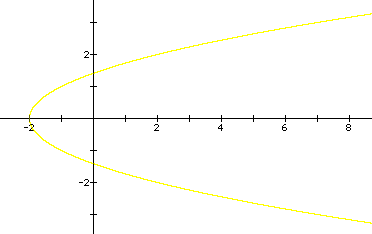

Write a short paragraph outlining the similarities and differences of the graphs above. Which of these graphs are functions?
At this time, we will only concern ourselves with those parabolas that are functions. The group of mathematical rules that create parabolas that are functions are called QUADRATIC FUNCTIONS. Much of the remaining units will deal with the manipulation of these rules so that we can find out certain information or behavior about a particular quadratic function. We will do this both graphically and algebraically.
It is often helpful to
find the mathematical rule that defines a parabolic data set.
For example, if we know that the rule for the parabola that corresponds
to the data in Unit 1 is given by ![]() where h(t) is the height of our projectile in meters at time t
(in seconds), we could determine the height of the projectile
at any time. Or, we could find the time it will take for the projectile
to reach a specified height. We will address each of these problems
in subsequent units.
where h(t) is the height of our projectile in meters at time t
(in seconds), we could determine the height of the projectile
at any time. Or, we could find the time it will take for the projectile
to reach a specified height. We will address each of these problems
in subsequent units.
First, however, we will address the problem of finding a rule for a data set (like the data set in Unit 1) that appears parabolic in nature.
The most basic rule for
a parabola is ![]() or using function notation,
or using function notation,![]() . We will call this rule the "parent
function" for quadratics. Sketch the graph of the parent
function by plotting points. Use an Excel Spreadsheet and Excel's
Chart Wizard to create a connected scatterplot. Does your graph
have a maximum or a minimum? The maximum or minimum point of a
parabola is called the VERTEX. Write the coordinates of the vertex
of the parent function. Does this function have any x or y intercepts?
If so, write them down as well.
. We will call this rule the "parent
function" for quadratics. Sketch the graph of the parent
function by plotting points. Use an Excel Spreadsheet and Excel's
Chart Wizard to create a connected scatterplot. Does your graph
have a maximum or a minimum? The maximum or minimum point of a
parabola is called the VERTEX. Write the coordinates of the vertex
of the parent function. Does this function have any x or y intercepts?
If so, write them down as well.
Graph each of the following functions using a graphing utility and write a brief description of how each compares to the parent function.
Were these your observations ?
Now compare each of the following graphs to the parent function and write a brief description of the effect.
Were these your observations?
Describe the translations
of the following graphs as compared to the parent function ![]() and sketch each graph on a piece of graph
paper.
and sketch each graph on a piece of graph
paper.
1. 2.
Give the coordinates of the vertices of each of the graphs above.
Try this for your final
task of this lesson:
Given the following data set, find a rule that best fits the data.
| x | f(x) |
| 7 | 42 |
| 8 | 33 |
| 10 | 21 |
| 12 | 17 |
| 13 | 18 |
| 14 | 21 |
| 17 | 42 |
| 18 | 53 |
Take all of your notes and graphs and summarize what you have learned thus far regarding transformations of quadratic functions.
Move on to Unit 3 - Graphing Quadratic Functions Through Transformations: Part 2.