In the Unit 7 we learned that we could use the completing the square process in order to convert a standard form quadratic function into vertex form. This process was somewhat laborious. In this unit we will introduce to shortcuts that we can take in order to locate the vertex of a parabola. The first will use the concept of symmetry in parabolas. The second will use an algebraic comparison of the two different forms of quadratic functions that we have studied thus far to find a quick formula for the coordinates of the vertex of a parabola.
Method 1.
If we can determine the values of the x intercepts, we can use symmetry to determine the x coordinate of the vertex. The x coordinate of the vertex will be the center of the two intercepts. The illustration below should help us visualize this.
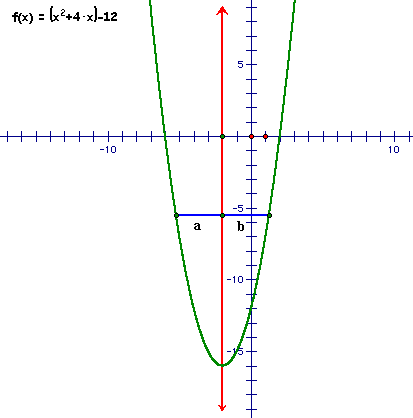
The vertical red line represents
the axis of symmetry which goes directly through the vertex. If
we draw a line perpendicular to the axis of symmetry that intersects
the parabola at any two points, the distance from the axis of
symmetry to either point will be the same. In the illustration
above, the length of segment a is equal to the length of segment
b. This being the case, the midpoint of the segment connecting
the two roots of the function will be the x value of the vertex.
Using the function 
above, we can find
the roots of the equation either by factoring or by using the
quadratic formula. Factoring the equation 
gives us 
. Using the Zero Products Property,
we know then that x+6=0, so x=-6. or x-2=0, so x=2. Now we can
use the midpoint formula 
in order to find
the x coordinate of the vertex. Once we have the x coordinate
(x=-2 in this case), we can plug this value back into the function
to find the corresponding y value of the vertex
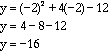
Thus the vertex of the function
has the coordinates (-2,-16).
The minimum value of this function therefore is -16.
Method 2.
The second shortcut method for finding the coordinates of the vertex of a parabola is even quicker, but the reason it works is a little more complex. Let's compare the general vertex form of a quadratic function with the general standard or polynomial form.
Vertex Form Standard Form Expanding the vertex form we get the following
Notice the coefficient of the x
squared term is a, the coefficient of the x term is -2ah, and
the constant term is the remaining expression in parentheses.
Notice also that in expanding the vertex form of the function,
we have converted it into standard form. Therefore, the coefficients
must agree. It follows that a = a, b =-2ah, and 
.
Because 
,
Remembering back to Unit
3 where we learned that (h,k) was the vertex in the vertex
form equation, we now once again know the x value of the vertex.
In this case we can confirm once again that in the function , the x value of the vertex is given by;
Once again, this information allows us to plug into the function to find the y value of the vertex to be -16.
In the next unit we will look at the connection between the factored form of a quadratic function and the zeros of that function.
