

The following is an investigation of the parametric curves of the form:
where 0 <= t <= 2*pi and d>=1
Let's examine the parametric curve when d=1. To see a graphing calculator picture of the curve of this type when a=b, click here. Notice that the curve is a circle with radius of a. What happens when a < b? The following is a graph when a=2 and b=4. Notice that the ellipse intercepts the x-axis at the positive and negative values of a and intercepts the y-axis at the positive and negative values of b.
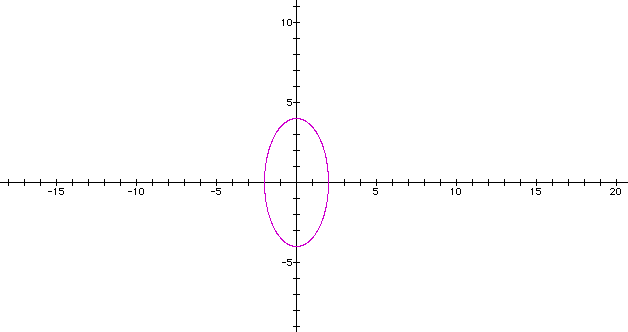
Can you make a guess about what will happen when a>b? The following is a graph when a=5 and b=3.
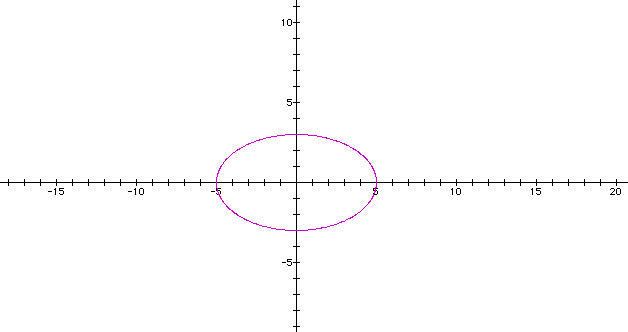
Now, let's investigate what happens when d=2. To see a graphing calculator picture of the curve of this type when a=b, click here. In this notice that the graph is only in the first and second quadrants when a=b. Again, notice the x-intercept and y-intercept in relation to a and b. What happens when a<b? The following is a graph when a=-3 and b=5. Notice that we can make the graph be in the third quadrant by making a negative and b positive. From this graph could you determine what would happen when a>b? Click here to see if you are correct.
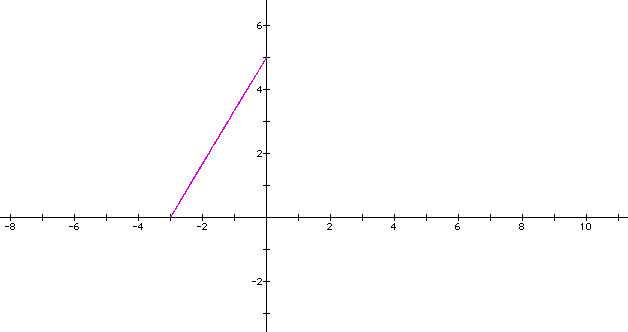
Let's look at the parametric curve when d=3. When you look at the graphing calculator picture of the curve for a=b, you notice that the curve is in all 4 quadrants. What happens when a<b? Can you guess what will happen when a>b?
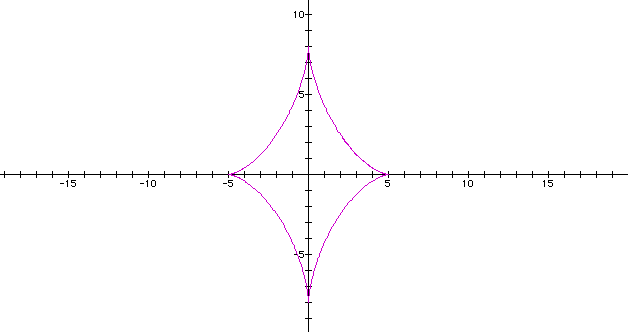
Let's look at the parametric curve when d=4. When you look at the graphing calculator picture of the curve for a=b, again notice that the curve is only in the first and third quadrants as it was when d=2. What happens when a<b? Below is a graph for a=-6 and b=15.
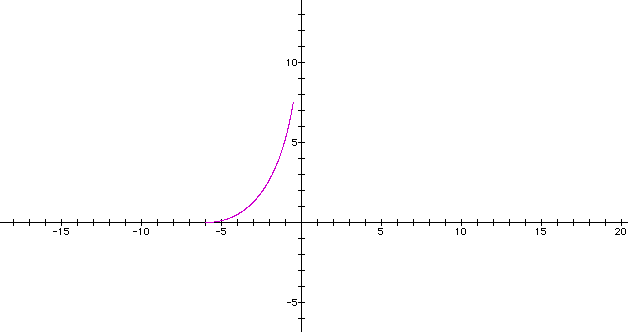
How does the graph above for a<b differ from the graph below where a>b? Below a=15 and b=-6.
