

For any triangle, ABC, and a point P inside the triangle, segments can be constructed through P and each vertex. The segments will intersect the side of the triangle opposite the vertex they pass through. The intersection points are D, E, and F. The following triangle is an example of this construction.
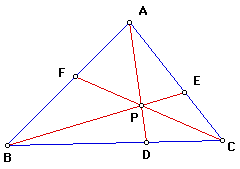
If you take the ratio [(AF)(BD)(CE)]/[(BF)(CD)(AE)], it will always equal one, no matter where you move point P inside the triangle.
If you construct two triangles on any one of the three sides of triangle ABC where the sides are parallel to the original sides of ABC, the two triangles will be similar. Let's look at the following picture as an example.
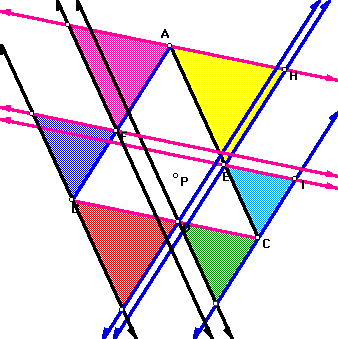
Above, all of the shaded triangles are similar to each other. Lines of the same color are parallel to each other. To see a GSP sketch that measures the angles to show similarity, click here.
To prove the similarity of the trianlges, consider the following picture.
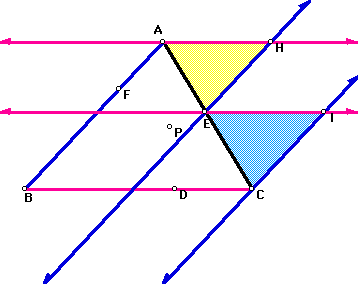
For triangle ABC with a point P inside the triangle, construct point D, E, and F as described above. Construct line AH such that it is parallel to BC and passes through point A. Construct line EI such that it is parallel to BC and passes through point E. Construct line EH such that it is parallel to AB and passes through point E. Construct line CI such that it is parallel to AB and it passes through point C. Angles AHE and HEI are equal since they are alternate interior angles (using the parallel lines AH and EI cut by the transversal EH). Angles HEI and EIC are equal since they are alternate interior angles (using lines parallel lines EH anc IC cut by the transversal EI). So angles AHE and EIC are equal. Angles AEH and ECI are equal since they are corresponding angles for the parallel lines EH and CI cut by the transversal AC. Then since the angles of a triangle sum to 180 degrees, the third angles of the two triangles are equal, thus angles HAE and IEC are equal. By angle-angle-angle similarity, triangles HAE and IEC are similar. The same argument would be made to show that the triangles made on sides BC and AB are similar.
This can be generalized to show that the triangles are still similar, even if point P is outside the triangle. For a working GSP sketch of when point P is outside of the triangle, click here.
When P is inside the triangle, the ratio of the area of triangle ABC to the area of triangle DEF is always greater than or equal to four. Below is a picture of the two triangles.
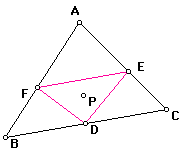
Click here for a demonstration that shows that shows the ratio of the areas. The ratio is equal to 4 when the points D, E, and F are the midpoints of the sides of triangle ABC and thus point P would be the centroid. Thus, triangle DEF would be the medial triangle of triangle ABC in this case.