

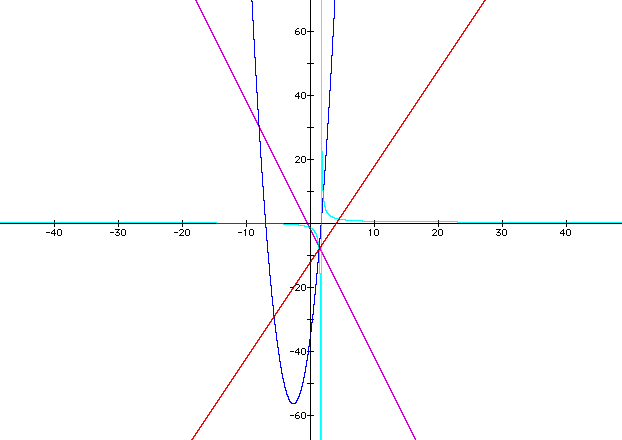
i. in this case all of the graphs intersect at a point,
ii. both of the slopes in the original equations f(x) and g(x) are negative, however the graph of f[g(x)] has a positive slope
iii. the parabola opens upward
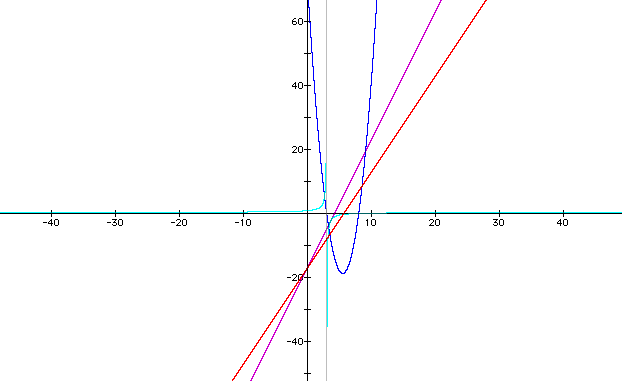
i. in this case the lines intersect, both of the lines intersect the parabola at two distinct points, the lines intersect the hyperbola at different points, and the parabola and the hyperbola intersect
ii. both of the slopes in the original equations f(x) and g(x) are positive as are the slopes of the composite functions
iii. the parabola opens upward
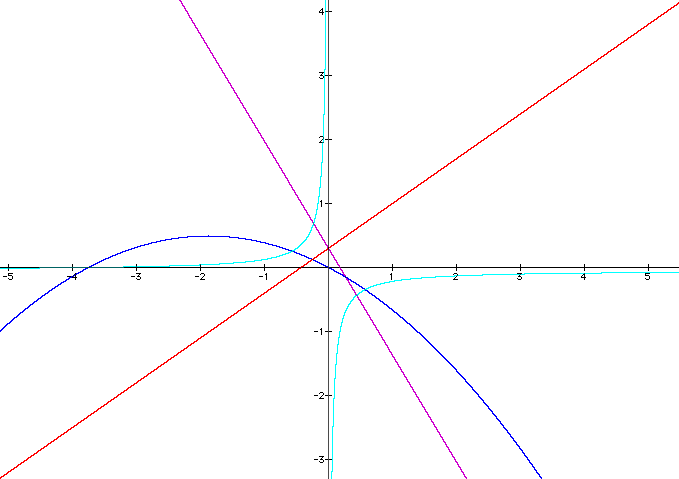
i. in this case the lines intersect, both of the lines intersect the parabola, and the lines intersect the hyperbola at two different points, and the parabola and the hyperbola intersect
ii. both of the slopes in the original equations f(x) and g(x) are positive as are the slopes of the composite functions
iii. the parabola opens downward
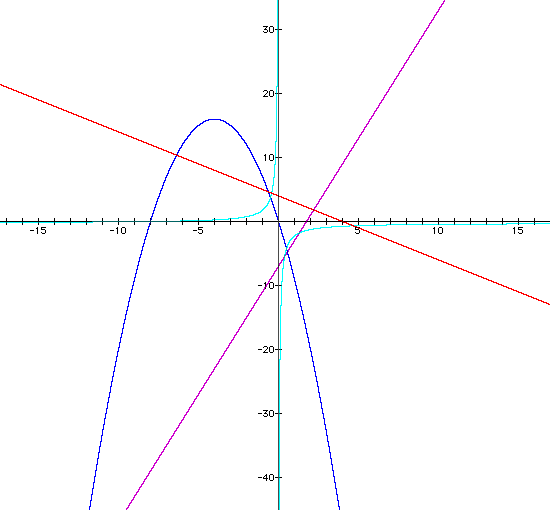
i. in this case the lines intersect, both of the lines intersect the parabola, and the lines intersect the hyperbola at two different points, and the parabola and the hyperbola intersect
ii. both of the slopes in the original equations f(x) and g(x) are positive as are the slopes of the composite functions
iii. the parabola opens downward because the coefficient on x is negative.
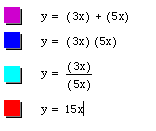
1. If f(x) = m1x+b1 and g(x) = m2x+b2, are linear:
i. then the graph of f(x) + g(x) = (m1x+b1)+(m2x+b2) = (m1m2)x + b1b2, is also linear,
ii. then the graph of f(x)g(x)=(m1x+b1) (m2x+b2) = m1m2xx + (b1m2+b2m1)x + b1b2 is similar to equation of a parabola,
iii. then the graph of f(x)/g(x) = (m1x +b1)/(m2x + b2), which resembles an equation of a hyperbola except when b1 and b2 equal zero, then it's linear,
iv. then the graph of f[g(x)] = f(m2x +b2) = m1(m2x + b1) + b2, is also the graph of a line.
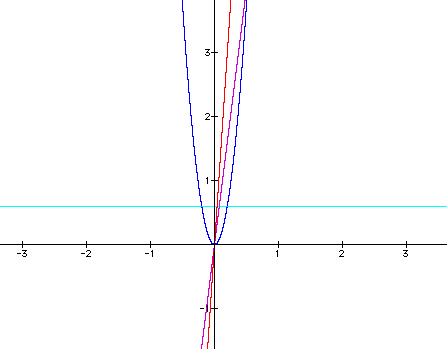
2. The lines intersect each other as well as the parabola and the hyerbola.
3. The parabola either opened upward or downward.
4. The hyperbola has line symmetry.