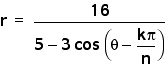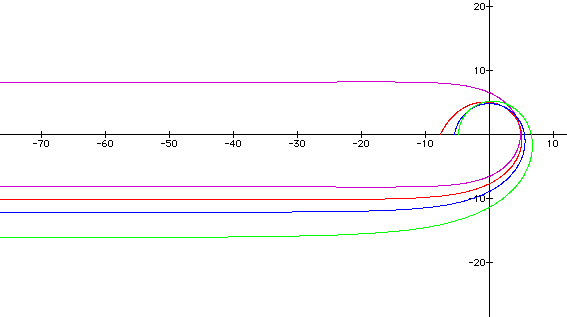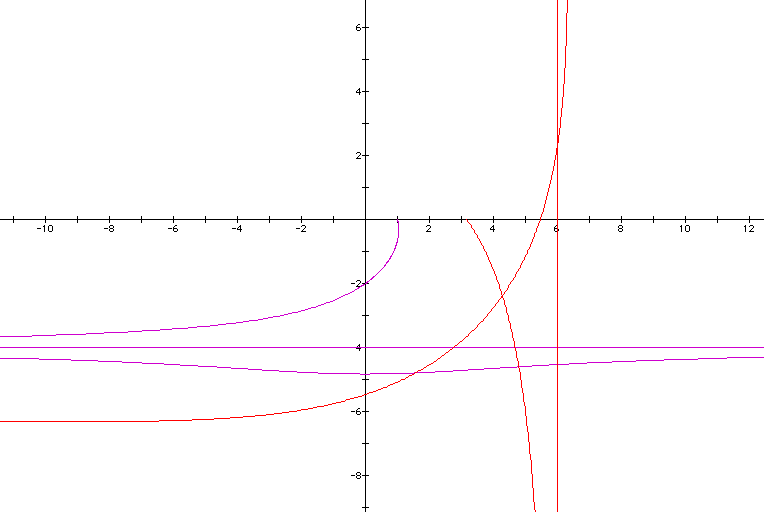Assignment 11 Problem 4 for Kanita DuCloux

For this assignment, I will investigate

Let's consider only the graphs of the form

 

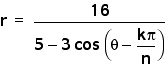where k is any integer and n is an even integer (n not equal to 0).

All the graphs are ellipses that are tangent to and lie inside the circle

. They all cross the x and y-axes.

 

 

Now, consider the graphs of the form

 

These graphs were interesting. Let's examine a few.

 

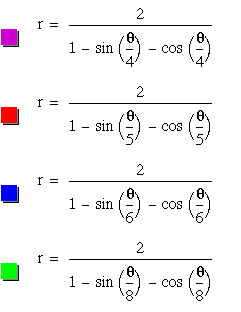
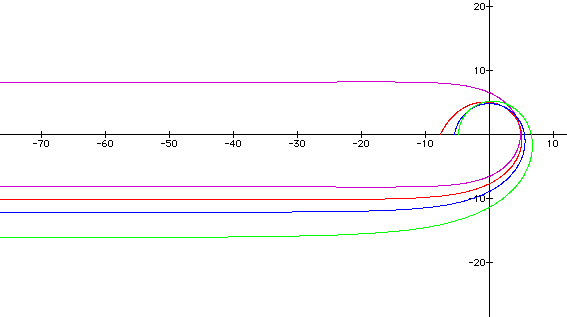When the denominator is 4, the graph does not touch he x-axis again after it crosses it once. The other graphs all touch the x-axis again and stop.

 

Let's observe a few more.

 

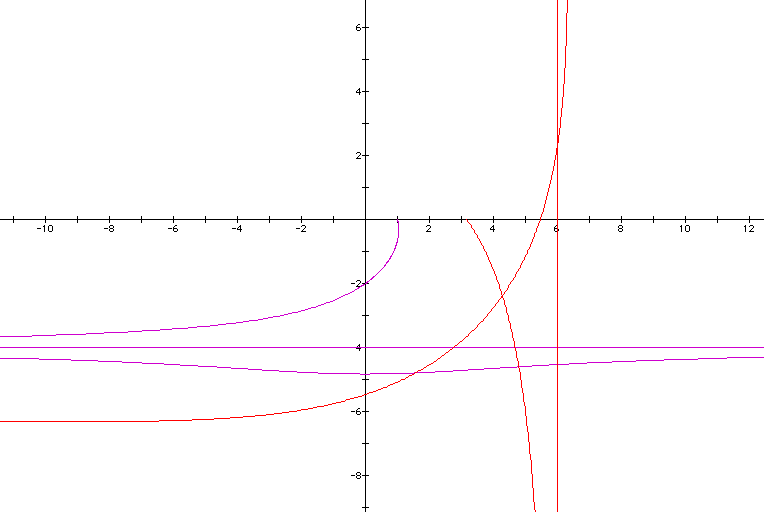I reaally don't know what to make of these. They appear to have asymptots but one graph crosses the asymptote. The graph intersects itself. They both have a partial piece to the graph that does not intersect the x-axis and then a piece along the asymptote. Interesting!

 

return