
Write-up #4 Problem 1 - Kanita DuCloux
Make a GSP script for the CENTROID
(G) of a triangle - the common intersection of the three medians.
A median of a triangle is the segment from a vertex to the midpoint
of the opposite side. Explore its location for various shapes
of triangles.
The centroid is always inside of the
triangle.


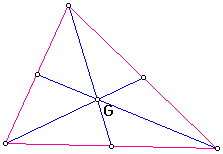
The ratio of the lengths of the vertex
to the centroid and the length of the side is always 2/3 = 0.667.

Click on 'centroid' below and give three points
and GSP script will find the centoid of the triangle formed by
the three points. Choose any vertex and move it around to observe
the ratios. Move the centroid, G, to see what happens.
Centroid.
Click on animation
to see an animation of a centroid and the relationship between
the ratios mentioned above.
return





