
Assignment 7 - Problem #1 for Kanita
Ducloux
Tangent Circles
Prepare a retrospective summary of
the following problem:
Given two circles and a point on one
of the circles. Construct a circle tangent to the two circles
with one point of tangency being the designated point.
Frustrating! Hair pulling! Problematic!
That's how I would describe this problem.
I took notes on the lesson and even asked Dr. Wilson for help.
But I was still lost. So, after much prayer, meditation, studying
my notes, and trying to recall my discussion with Dr. Wilson,
I was finally able to do something similar to the what Dr. Wilson
illustrated.
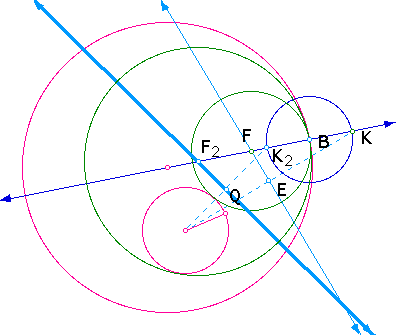
1. Draw a circle within a circle
and a point (B) on one of the circles.
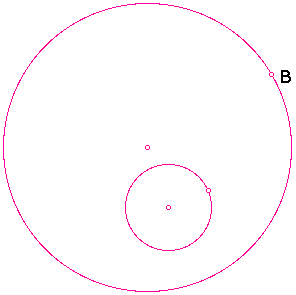
2. Find the radius of the small
circle and construct a circle of the same radius with point of
trangency (B) being the center of the new circle.
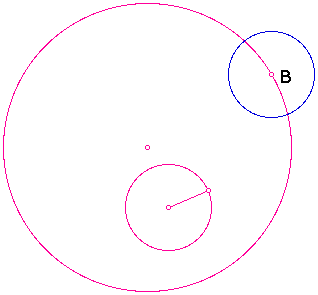
3. Construct a line through the
center of the large cirlce and the point of tangency (B).
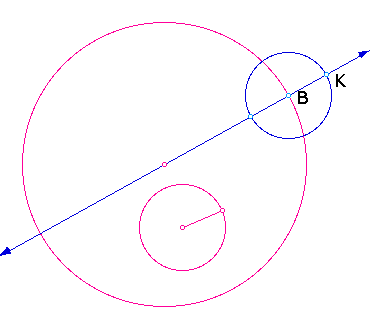
4. Construct a segment connecting
K to the center of the original small circle and find the midpoint
(E).
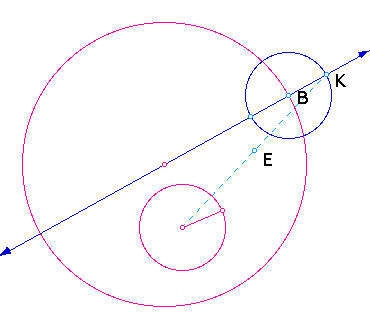
5. Construct the perpendicular bisector
of the segment. The intersection of the perpendicular bisector
and the line connecting B to the center the of the original small
circle is point F.
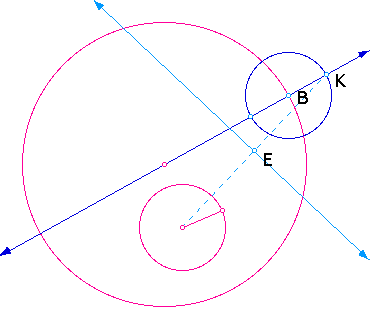
6. Finally, construct the tangent
circle with center F and point of tangency B.
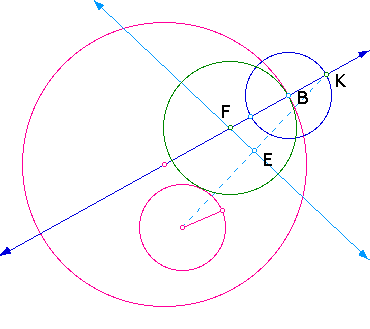
After all of that, I thought I was
finished until I discovered that there was another such circle
tangent to the two given circles. How do I find it? I should be
able to use what I've already done. There should be a relationship
between the two circles. Let's see what I found.
In step 4, instead of connecting
K to the center of the original small circle, connect to the second
point of intersection (K2).
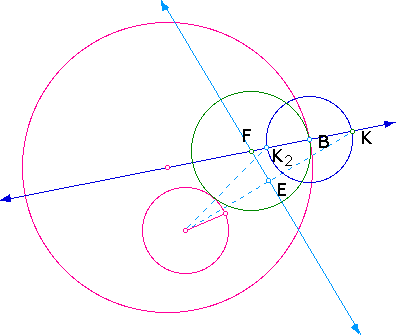
5B. Construct the perpendicular
bisector of the segment. The intersection of the perpendicular
bisector and the line connecting B to the center the of the original
small circle is point F.
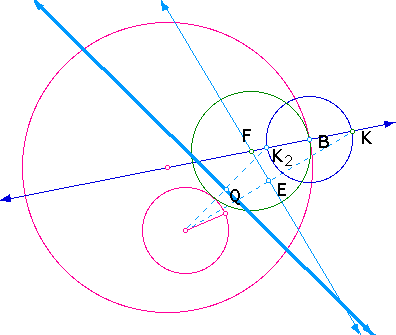
6. Finally, construct the tangent
circle with center F2
and point of tangency B.
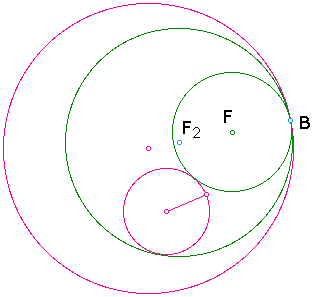
Let's look at the picture without
all of the lines. The two green circles are the tangent circles
at Point B.
I was glad when I finallly finished
this problem.
return











