
Assignment 8 Problem 1 for Kanita DuCloux
For this assignment, I will:
1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle
ABC.
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
6. Construct the Circumcircles of triangles
ABC, HBC, HAB, and HAC.
7. Conjectures? Proofs?
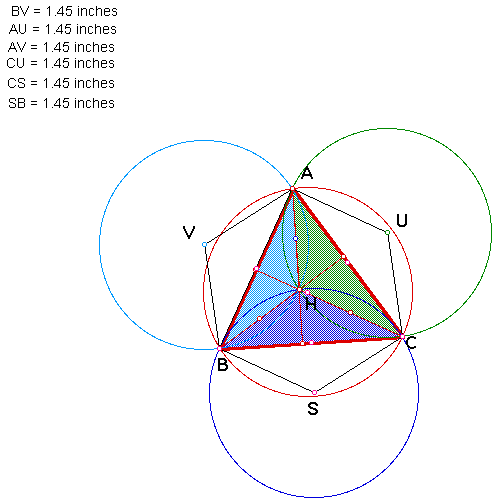
Observe a few of the constructions.
The orthocenter of triangle HBC is
vertex A (of the original triangle), the orthocenter of triangle
HAB is vertex C (of the original triangle), the orthocenter of
triangle HAC is vertex B (of the original triangle).
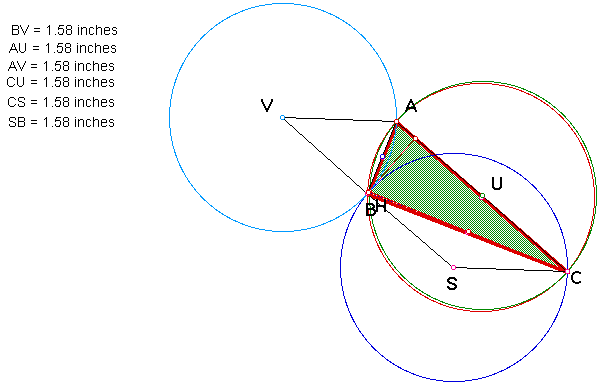
Observe what happens when triangle
ABC is a right triangle. The orthocenter(H) of triangle ABC is
at the right angle, B. The circumcircles of triangles ABC and
AHC appear to coincide. The center of the circumcircle of triangle
AHC, U, is also the center of the circumcircle of triangle ABC.
The measures show that the radii of
all of the circumcircles are equal. Also, the area of triangle
ABC and the triangle formed by the connecting the centers of the
circumcircles (SUV) are equal. The area of circumcircles are equal
which follows from the radii all being equal.

Click orthocenter
to construct one.
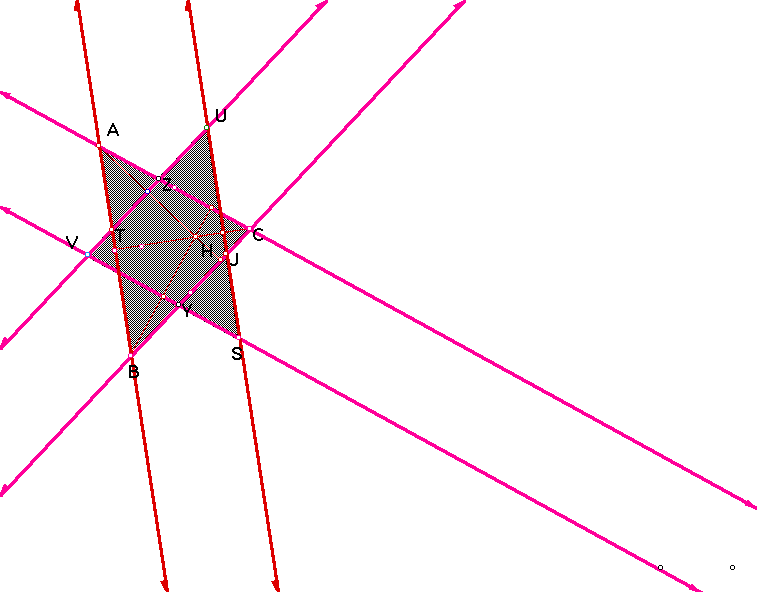
First construct parallel lines. The
following angles are conguent:
<TVB and <VYB, <ZCY and <CYS,
since <VYB and <CYS are vertical angles, <TVB is congruent
to <ZCY.
<SUZ and <ZTA and <VTB and
<TBY, since <ZTA and <VTB are vertical angles, <SUZ
is congruent to <TBY.
Since, BC and UV are congruent, trianle
ABC is congruent to triangle SUV by ASA.
return





