Final Project for Kanita DuCloux

Part A: I will consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. Then, explore (AF)(BD)EC) and (FB)(DC)(EA) for various triangles and various locations of P.

Observe the triangle below. (AF)(BD)EC) = (FB)(DC)(EA). Click on triangle to construct a triangle like the one below and drag a point to see that the two products are always equal.

 

 

Part B: Prove (AF)(BD)EC) = (FB)(DC)(EA)

To prove this, I need to draw some parallel lines to produce similar triangles and consider the ratio

and generalize to a point P outside the triangle.

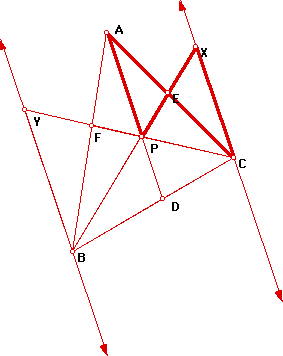
Draw lines (BY and CY) parallel to AD. Now, triangles BPD and BXC are similar by AA AND

We also have triangles CPD similar to triangle CYB and thus

 

Taking the proportions above, we have

,

yields, (BD)(XC) = (BC)(PD) and (DC)(YB) = (PD)(BC). By substitution, we get

(BD)(XC) = (DC)(YB) or .

 

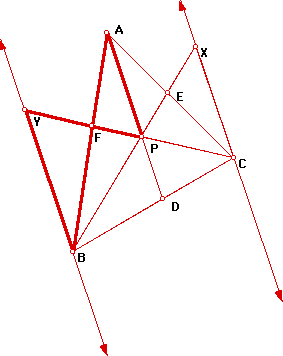
Next we have, triangle EXC similar to triangle EPA by AA. Going through a similar process, yields

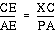
We also have triangle FPA similar to triangle FYB by AA and

Let's revisit our proportions:

,,

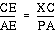Everything on the right-hand side of the equation cancels out and therefore equals 1. So,

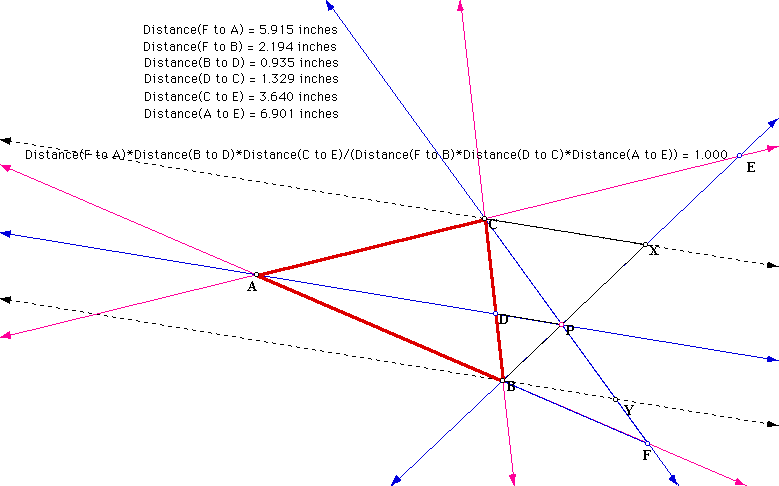
Can this be generalized so that P is outside of the triangle? Observe the pictures below. There are a lot of lines in the pictures but look at the distances. It appears that the same is true if the point P is outside.

Then, click outside to try it yourself.

 

 

 

 

 

Part C: Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?

Observe the following picture. Then, click on area and drag a vertex to see what happens.

 

When is the ratio equal to 4? Look and see. Point P is the centroid.

 

 

return