Part One. Please
see Write-Ups #1-12. ![]()
Part Two.
A. Consider any triangle ABC. Select any point P inside triangle ABC and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
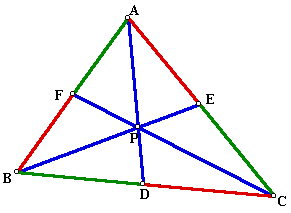
Explore (CE)(BD)(AF) and (EA)(DC)(FB) for various triangles and various positions of P.
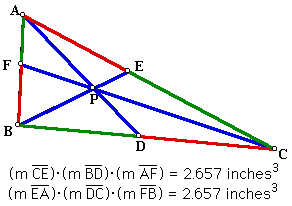
Conjecture: The products above appear to be equal for any triangle ABC and for any position of P. Below is a diagram displaying one case. To explore multiple cases (multiple types of triangles and multiple positions of P), download this GSP file.
B. Proof: To prove that the products of the segments above must be equal, consider drawing some auxilliary lines parallel to AD and passing through B and C. Extend CF to intersect the parallel at M as shown below, and extend BE to intersect the parallel at N as shown below.
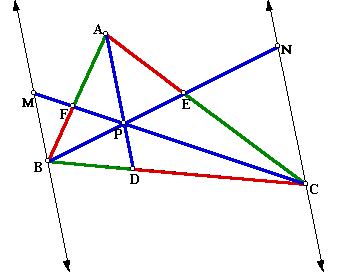
Many similar triangles are created!
(i) First consider triangles BDP and BCN, which are similar by the angle-angle similarity theorem, AA (angle PBD is shared, and corresponding angles BDP and BCN are congruent, as are corresponding angles BPD and BNC, since NC is parallel to PD.) From these triangles a key relationship is:
(ii) Also consider similar triangles CPD and CMB (which are similar by the same reasoning in (i).) A key relationship from these triangles is:
These two proportions reveal that (BC)(PD) = (BD)(NC) = (DC)(MB).
(iii) In addition, consider triangles BMF and APF, which are similar by AA (angles MFB and PFA are vertical, and both other pairs of angles are alternate interior angles, which are congruent since MB is parallel to AP.) From these triangles a key relationship is:
(iv) Finally, consider similar triangles APE and CNE (which are similar by the same reasoning in (iii).) From these triangles a key relationship is:
Substituting MB and NC into the relationship (BD)(NC) = (DC)(MB) from (ii) yields
The measure AP can be divided out on each side. Furthermore, multiplying by EA and AF reveals that
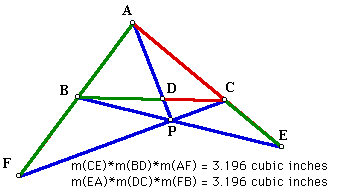
Furthermore, the results can be generalized so that P can lie outside the triangle, as you can see in the diagram below. Download this GSP sketch to explore further.
C. Show that when P is inside triangle ABC, the ratio of areas of triangles ABC and DEF is always greater than or equal to 4. When is it equal to 4?
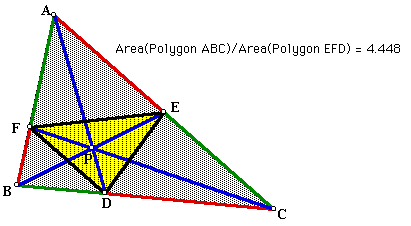
This GSP sketch reveals that the ratio of areas does always appear to be greater than or equal to 4, and that the ratio is equal to 4 when D, E, and F are midpoints of the sides of triangle ABC, and P is therefore the centroid of triangle ABC.
(1) It is relatively easy to show that the ratio is equal to 4 when D, E, and F are midpoints and P is the centroid.
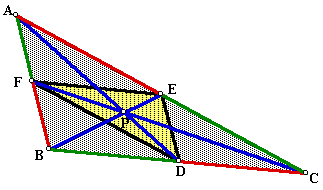
Proof: In the diagram above, D, E and F are midpoints of BC, AC, and AB respectively. Thus P must be the centroid of triangle ABC because P lies on all three medians.
Triangles AFE are ABC are similar by the SAS Similarity Theorem with a scale factor of 1/2 (note that angle A is shared by both triangles.) Thus FE = 1/2(BC).
Similarly, triangles FBD and ABC are similar, and so FD = 1/2(AC), and triangles EDC and ABC are similar to ED = 1/2(AB).
Thus, triangles DEF and ABC are similar by the SSS Similarity Theorem with a scale factor of 1/2. By the Fundamental Theorem of Similarity, the ratio of their areas must be (1/2)^2 = 1/4.
(2) If P is "pulled away" from the centroid, then triangle DEF will not necessarily be similar to triangle ABC. Furthermore, exploration with GSP supports the idea that the area of triangle DEF reaches a maximum value when D, E, and F are at the midpoints of the sides of triangle ABC. I have not yet arrived at a proof of why this relationship must be so.