Exploring with the Nine-Point Circle

...a few answers and some more questions...

The center of the Nine-Point Circle (N) has a special relationship to the triangle ABC. What is that relationship? Are there any other relationships you can find between N and other special triangles (i.e., the medial triangle or orthic triangle)?

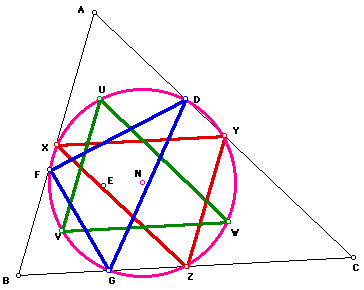
The center of the Nine-Point Circle is the circumcenter of the medial triangle XYZ, of the orthic triangle DFG, and of the triangle formed by connecting points U, V, and W. Therefore, we have another definition of the Nine-Point Circle as the circle that is the circumcircle of these three triangles.

Download a GSP sketch to explore these triangles.

Return to Amy's Write-Up #4.

What happens to the Nine-Point Circle when the triangle is right?

When the triangle is right, the feet of two of the altitudes coincide with the vertex of the right angle of the triangle. In addition, the feet of two of the midpoints of segments drawn from the vertices to the orthocenter coincide with the the midpoints of the legs of the right triangle.

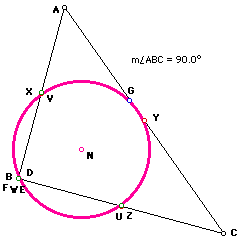
The reason for these sets of coincident points is that in a right triangle, the legs are altitudes drawn from the acute angles of the triangle (see segments AB and CB below.) So, the feet of these two altitudes (D and F) meet at the vertex of the right angle, B.

And the midpoints of the legs of the triangle (points X and Z) coincide with the midpoints of the segments drawn from the vertices A and C to the orthocenter E (points V and U) because the orthocenter lies at the vertex of the right angle. Furthermore, the "midpoint" of the segment from vertex B to the orthocenter E "disappears" because B and E coincide (so point W also coincides with them.)

Therefore, a total of five points appear to be on the circle. The orthocenter coincides with the vertex of the right angle. Here's a conjecture to explore and verify: the center of the Nine-Point Circle, N, lies inside the triangle, collinear with the midpoint of the hypotenuse (Y) and the vertex of the right angle, B (both of which lie on the Nine-Point Circle.)

Can the orthocenter (E) and center of the Nine-Point Circle (N) ever coincide? If so, what happens to the triangle when they do? If not, why not?

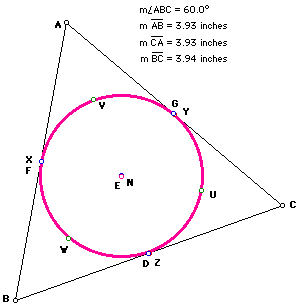
When the orthocenter and center of the Nine-Point Circle coincide, the triangle becomes equilateral (see below.) Notice that now there appear to be six points on the circle, because the feet of the altitudes (points D, F, and G) coincide with the midpoint of each side of the triangle (points Z, X, and Y.) Here's another conjecture: the six points are equally spaced around the circle.

Return to Amy's Write-Up #4.

Determine what types of triangles are formed and how many of the nine points are distinct when

-the orthocenter (E) is outside but the center of the Nine Point Circle (N) is inside the triangle;
-E coincides with a vertex of the triangle;
-N coincides with a vertex of the triangle;
-E and N are both outside the triangle
-E and N are both inside the triangle;
-N is outside but E is inside.

Please use the GSP file to explore and view each of the following conclusions:

-When E is outside and N is inside, the triangle is obtuse and all 9 points may appear distinct.
-We have seen that when E coincides with a vertex of the triangle, the triangle becomes right and 5 points appear distinctly (see above.)
-When N coincides with a vertex of the triangle, an obtuse isosceles triangle results, and 6 points appear distinctly. (Try it!)
-When E and N are both outside the triangle, the triangle is even "more obtuse!" than when only E is outside, and all 9 points may appear distinct. (Try it!)
-When E and N are both inside the triangle, the triangle is scalene as we have seen, and all 9 points may appear distinct.
-N cannot lie outside with E inside...think about it...the moment N lies outside the triangle, the triangle must be obtuse, which forces E to lie where? Try it out!

Return to Amy's Write-Up #4.