Exploring a Triangle made of Medians

Assignment #6 for EMAT 6680, by Amy Hackenberg

Here's the Problem:

Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., Are they congruent? similar? Do they have the same area? the same perimeter? Are their ratio of areas constant? Are their ratio of perimeters constant?) Prove what you find.

Exploration Part I: Making the construction.

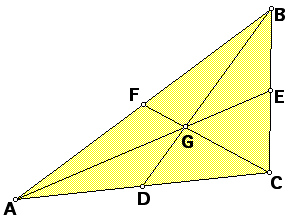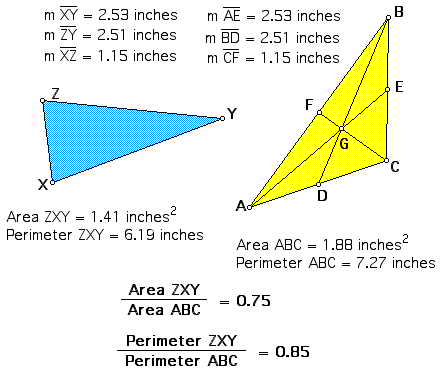
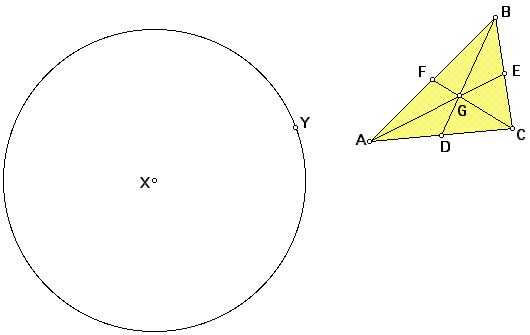
First of all, it is necessary to create a triangle with the medians drawn in as shown at left. Of course, the point where the medians intersect is the centroid, G, and 2GE = GA; 2GF = GC; 2GD = GB. To create the triangle with the three sides having the lengths of the three medians, you can start by placing a point on the same sketch, selecting the point and one of the medians. For example, place point X and select X and segment AE, as in the sketch below. Construct a circle by center (X) and radius (AE) to create a locus of points around X with length equal to AE. Place a point Y on the circle. XY = AE, and XY will form a side of our new triangle.

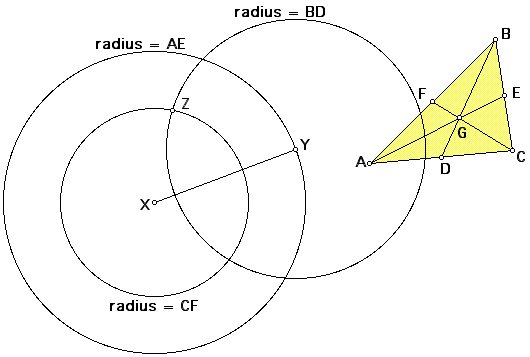
Now, select point Y and another median BD. Construct a circle with center (Y) and radius (BD). Then select point X and median CF to make a final circle. The intersection of these two circles will locate point Z, the third vertex of the triangle formed by sides equal to the length of the medians of triangle ABC.

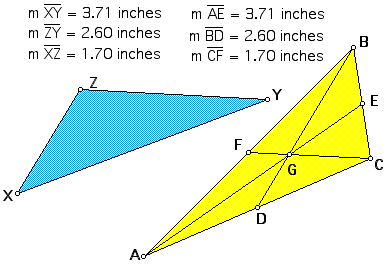
Draw triangle XYZ, hide the circles, and measure to confirm our construction.

To the Top

Return

Exploration Part II: Finding a relationship.

With a little dragging and measuring, it's clear that the two triangles are neither congruent nor similar. Their areas and perimeters are not equal. But the ratio of the areas of triangle XYZ to triangle ABC appears to remain constant (although the ratio of perimeters does not.) My conjecture (see below) is that the ratio of the areas of the two triangles (the triangle with side lengths equal to the median to the original triangle) is 3/4. Therefore, the blue triangle has three-fourths the area of the yellow trianlge. Hmm!

Download this GSP sketch to play around with this relationship and maybe to discover others.

To the Top

Return

Exploration Part III: PROVING the relationship. (Here's one way...)

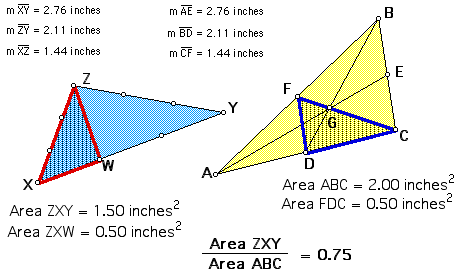
First of all, let's "simplify" the problem. We know that the medians of the triangle are split into ratios of 2:1 by the centroid, point G. So, identify those points (by the way, I used my trisection sketch here) on triangle XYZ. Then, draw FD in triangle ABC.

Essentially, to prove the above area relationship, we need to show that the area of triangle XZW (which is one-third the area of triangle XYZ) is equal to the area of triangle FDC (which is one-fourth the area of triangle ABC.) How do I know this information?

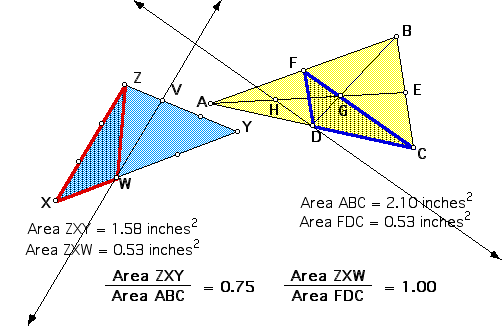
Notice that the triangles XZW and FDC are not congruent, although XZ = CF. (In particular, XW = (1/3)AE = GE, which is not necessarily equal to FD or DC.) Therefore we cannot use congruent triangles to show equal areas. Instead, we can show that the triangles have the same area if the heights drawn from W to XZ and D to FC are equal. (Because triangles with the same base and same height obviously have equal areas.)

Furthermore, the height for triangle XZW equals the distance between XZ and the line parallel to XZ through point W; the height for triangle FDC equals the distance between CF and the line parallel to CF through point D.

Now, the line drawn through D is parallel to CF and passes through the midpoint (D) of AC. Therefore, this line must pass through the midpoint of AG, point H. Similarly, the line drawn through W parallel to XZ cuts XY into a ratio of 1:2 (XW:WY), so it must cut ZY in the same ratio, and therefore ZV:VY = 1:2.

This information is important because XY = AE, and so (1/3)AE = XW = HG. In the picture below, I have drawn in the heights (TW and DJ) and two other segments, SW and FH. Notice that XS = FG because both are one-third of median CF = XZ. Also, SW = ZV = (1/3)BD, and FH = GD = (1/3)BD. So SW = FH. How do I know this information?

Therefore, the small triangles, XSW and GFH are congruent. Consequently, their altitudes must be congruent--which is the distance between the lines (the green distance), as desired.

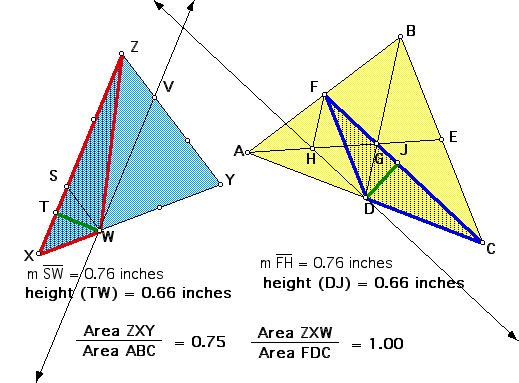
THUS, triangle XZW and triangle FDG have the same area, since XZ = CF by construction, and since the heights of the triangles drawn to these bases are equal.

SO...the ratio of area of triangle XYZ to the area of triangle ABC is 3/4. !! QED.

If you'd like, download this GSP file to play with these triangles and segments a little bit more. There are some interesting "special cases" to explore when certain segments are aligned.

To the Top

Return