This write-up is a summary of this author's beginning exploration with tangent circles. In particular, the focus will be on the many different curves that "tangent circles can create" when certain points are traced and a point of tangency is animated along a circular path.
Of course, standard curves abound (ellipses, hyperbolas, circles), but there are some far more unusual shapes that may appear without much complexity of construction, and the appearance of these shapes may prove particularly interesting or provoking to students who are accustomed to seeing rather "regular-looking" curves in school mathematics (read: symmetrical, simple rather than crossed, etc.)
You can read through the paper linearly or jump around to the four main topics:
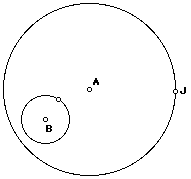
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

Of course, there are two such circles. In the diagram above, there is a circle through point J and tangent to circles A and B that lies outside circle B (except for the point of tangency), and another such circle that "contains" circle B (i.e., circle B lies in the interior of this circle, except for the point of tangency which is on this circle.) I suspect that pictures are clearer than words, so see the image on the left below.
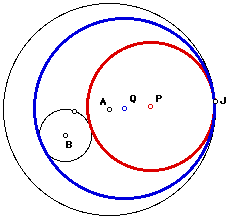
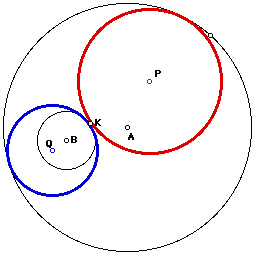
Circle P is the first circle described above; circle Q is the second. Notice that if we use point K on the smaller circle as the point of tangency, there are still two possible tangent circles, and they still satisfy the descriptions given above. However, in the case with J as the point of tangency (left diagram), circle Q and circle P are internally tangent. In the case with K as the point of tangency (right diagram), circle Q and circle P are externally tangent.
Below are the construction lines for the creation of circle P and circle Q with point of tangency J.
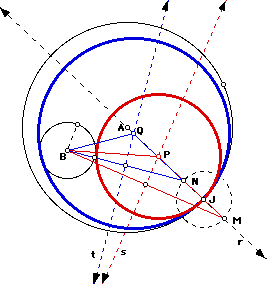
Notice that the centers of circles P and Q are found by constructing key isosceles triangles (triangle BMP and triangle BNQ.) In the case of creating the smaller tangent circle (circle P), we know that its center must be its radius plus the radius of circle B away from point B. And clearly P must lie exactly circle P's radius away from point J. Therefore, create a circle centered at J with the same radius as circle B. The distance from P to circle B + radius of circle B = the distance from P to J + JM, since JM equals the radius of circle B.
Therefore, P will lie on the perpendicular bisector of MB (line s, shown dashed in red), since all points on this line are equidistant from B and M. Point P must also lie on line r (dashed in black) because PJ must lie on the same line as AJ. Therefore, the intersection of lines s and r yields point P.
In the case of the larger tangent circle (circle Q), its radius consists of the diameter of circle B plus "some more." Since the distance from Q to point J must be the same as the distance from Q to circle B plus the diameter of circle B, the distance from Q to point N must be the same as QB. Therefore, create the perpendicular bisector of BN (line t, shown dashed in blue.) As with point P, Q must also lie on line r because QJ must lie on the same line as AJ. Therefore, the intersection of lines t and r yields point Q.
The procedure is essentially the same if we take point K on the smaller circle to be the point of tangency. You can see below that a circle congruent to circle A was replicated at the point of tangency, K (dashed in black.) The intersection points between this circle and line r that passes through B will help form the key isoceles triangles.
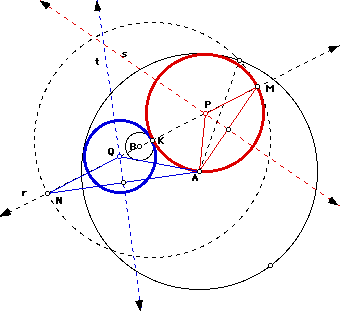
P must be equidistant from points A, K and M. Therefore draw either KA or AM (AM was drawn above), create the perpendicular bisector (line s), and find P at the intersection of lines s and r as before. Circle Q must have diameter equal to circle A's radius minus "something." The distance from K to N equals the radius of circle A, so the distance from Q to N must equal the distance from Q to A (i.e. both are circle Q's radius + the "something.") Therefore, Q is equidistant from N and A. Draw perpendicular bisector (line t) and find Q at the intersection of lines t and r as before.
[For more details and a step-by-step process, please go to Dr. Wilson's Assigment 7 for EMAT 6680.]
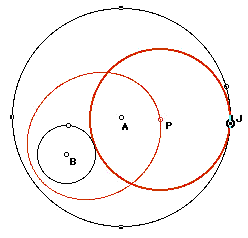
CASE I: Small circle contained in large circle.
When the point of tangency is animated around the circle (J around A in the two diagrams below) and the center of the tangent circle is traced, (P in the left diagram; Q in the right), ellipses result. Notice that the centers of the original circles appear to be the loci of the ellipses. The reason is not hard to discern from the construction diagrams above: The distance BP + PA = MP + PA, which is clearly constant (see Fig. 3 above.) Similarly, the distance BQ + QA = NQ + QA, which is also constant (see Fig. 3 above.)
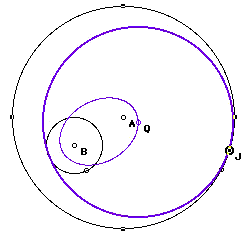
Notice that when K is used as the point of tangency, the same locus results. The diagram on the right shows that the ellipses are not similar.
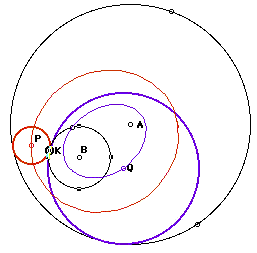

CASE II: Small circle OUTSIDE of large circle.
When the smaller circle is outside of the large circle and the center of the tangent circle is traced while the point of tangency is animated around a circle, a hyperbola results. This locus will occur for either circle P or circle Q (the circle that does not contain circle B or the circle that contains circle B), so only circle Q and the locus of its center is shown below. Again, the construction reveals why: BQ - QA = NQ - QA always, since BQ = QN. Furthermore, NQ - QA = AN, which is clearly constant (i.e. circle A is fixed.)

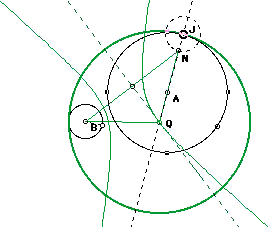
CASE III: Circles intersect.
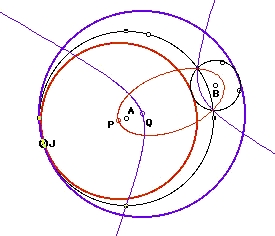
Aha--now it starts to get even more interesting. When the original circles intersect and point of tangency J is animated around a circle (circle A below), the locus of the center of circle P (the circle that did not contain circle B) is still an ellipse. But the locus of the center of circle Q is a hyperbola. Notice that the foci for both the ellipse and hyperbola are the centers of the original circle and that the ellipse and hyperbola pass through the intersection points of circles A and B.
|
|
Again, the construction is revealing. BP + PA = JP + PA = radius of circle A, which is constant. Thus the locus of point P is an ellipse. However, BQ - QA = NQ - QA = NA is constant. Thus the locus of point Q is a hyperbola. |
CASE IV: Circles are tangent (or close to tangency.)
There are four cases to consider when circles A and B are tangent: first, circles A and B can be internally tangent, and both circle P and circle Q (the circle that does not contain circle B and the circle that does) can be explored. Then circles A and B can be externally tangent, and again circles P and Q can be examined. Since in this paper I want to get on to some other interesting curves, please download these GSP files if you are interested in exploring this case.
GSP file for circles A and B internally tangent
GSP file for circles A and B externally tangent
Of course, you can take these downloads and rearrange circles, etc., to create any of the above situations. However, Cases I-III are summarized in this GSP file.
As this paper is intended to be a summary, in this section I will point out some interesting shapes created by tracing other points as the point of tangency is animated around a circle. However, I will not go into each possible case as thoroughly as in the above discussion (i.e., this section is just a taste of what is there to explore!)
Midpoints of the base of the key isosceles triangles.
As you can see below, the loci of the midpoints of the key isosceles triangles are circles that are tangent to the vertices of the loci (ellipse or hyperbola) of the corresponding center of the tangent circle.
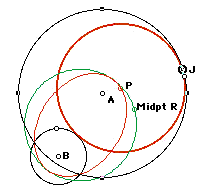
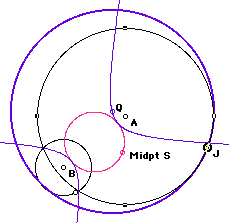
The construction (once again) reveals why the loci of the midpoints of the isosceles triangles are these special circles. Since the reasoning is the same in both cases, I will show only the construction for circle P below. Notice that the center of the green circle created by the locus of point R is point T below, the midpoint of AB. So, consider the triangle BMT shown in green. Notice that RT is a midsegment in that triangle, so it is always half of AM, which remains fixed as J moves around circle A. Therefore, TR will remain constant and will be the radius of the circle traced by point R.
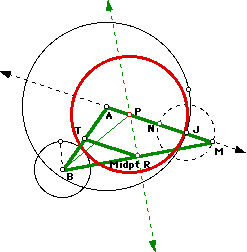
Download this GSP file to explore several configurations of circles A and B with these key midpoints traced.
Intersection points between tangent circle (circle P or Q) and certain lines.
In the figure below, the light blue line (c) passes through K (the point of tangency between P and B) and the center of circle A. The green line (d) passes through J (the point of tangency between P and A) and the center of circle A. Z is the other intersection point of c and circle P. Y is the other intersection point of d and circle P.
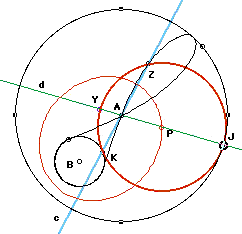
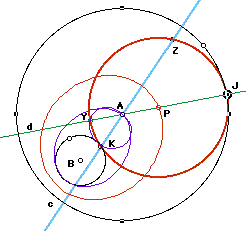
These curves are rather unusual--or at least not the sort most high school students see regularly. The locus of point Z looks like a "lopsided figure 8," where one loop resembles a rose petal from a polar graph and the other loop wraps tightly around circle B. The locus of point Y is also two loops, both of which appear elliptical.
Viewing the animation in action is actually much more exciting than looking at still pictures, so download this GSP file to view these curves, as well as a fish and a heart when circle Q is used.
Intersection points between a line perpendicular to the diameter of circle P or Q through a point of tangency.
Even stranger curves result in these constructions. View this GSP file and experiment!
Now we get to something especially neat: tangent circles can create a parabola. But the creation can be deceiving! This author uncovered the locus of a parabola through addressing this exploration: Given a line (j) and a circle with center K. Take an arbitrary point P on the circle. Construct two circles tangent to the given circle at P and tangent to line j.
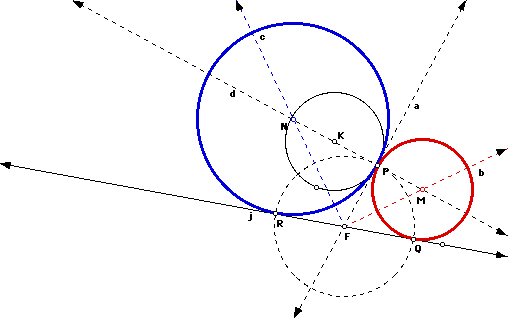
Both circles will be tangent to point P, and therefore their radii will be contained on line KP. The line perpendicular to KP ( line a, the tangent line to circle K at P) will also be tangent to both circles. Of course, the point where line a intersects line j, point F, is key because it will be the intersection of tangent segments to both circles.
Therefore, draw circle F with radius FP. The center of the red circle must be equidistant from P and Q; the center of the blue circle must be equidistant from R and P. Constructing isosceles triangles PFQ and PFR would work here and would be analygous to some of the constructions above. However, I chose to draw angles bisectors b and c. The intersection of ray b and line KP yields point M; the intersection of ray c and line KP yields point N. (M and N must be equidistant from line j and point P by definition of an angle bisector.) Ta da!
Note that M is always equidistant from a line (j) and a point (P). Likewise for N. So...examine the loci of M and N as P is animated around circle K. Why do TWO curves appear and are they parabolas?
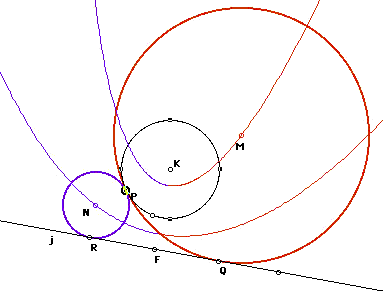
At first, I was sure that they were. But then as I began to try to justify the location of a focus and directrix for each one, I realized they are NOT parabolas. M is not equidistant from a fixed point and a fixed line but from a NON-fixed point (P) and a fixed line (j). Likewise for N.
The color switching on the curves has to do with the key moments when line KP is perpendicular to line j and when line KP becomes parallel to line j. To see the animation and explore further, download this GSP file.
Of course, the question remains--can tangent circles create a parabola? After you have downloaded the GSP file above, examine what happens to the locus of M and N when the distance between P and K approaches zero. Do you have your answer?