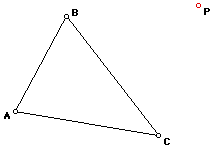
This paper (a sort of smorgasbord of observations and conjectures) attempts to address these four questions:
I. Definition. Given a triangle, what is a Pedal Point and its corresponding Pedal Triangle?
II. Special well-behaved cases. What special Pedal Triangle results when the Pedal Point is a special point (i.e. a center) of the given triangle?
III. Loci. What are some interesting loci of vertices of a Pedal Triangle when the Pedal Point is a special point (not necessarily a center) of the given triangle?
IV. A Special Investigation. What happens if a Pedal Point is animated around the incircle of the given triangle and the midpoints of the sides of the Pedal Triangle are traced? What if instead the excircle is used?
I. Given a triangle, what is a Pedal Point and its corresponding Pedal Triangle?
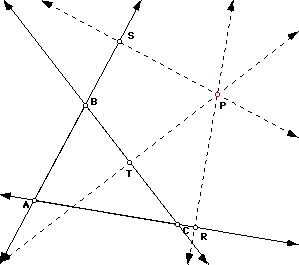
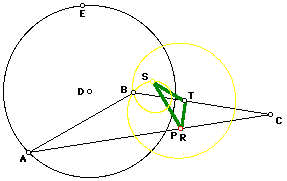
Given triangle ABC, and let P be any point in the plane. Construct perpendiculars from P to the sides of triangle ABC, extending the sides as necessary. (Notice that lines AB, BC, and AC have been drawn below in the diagram on the right.)


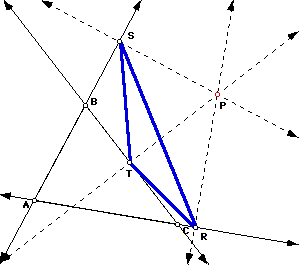
Connect the three intersection points R, S, and T to form a triangle, which is called the Pedal Triangle for Pedal Point P.
II. What special Pedal Triangle results when the Pedal Point is a special point (i.e. a center) of the given triangle?
(1) When the Pedal Point P is the circumcenter of the given triangle ABC, the Pedal Triangle is the medial triangle. The reason for this special result is that AB, AC, and BC are chords of circle P when P is the circumcenter. If a segment drawn from the center to a chord is perpendicular to the chord, it will bisect the chord. Hence R, S, and T must be midpoints of the sides of triangle ABC and so form the medial triangle of triangle ABC.
Notice that since the medial triangle always remains inside triangle ABC, all three vertices of the Pedal Triangle will always remain on the sides of triangle ABC--which is unusual (see diagram above in the Definition section, where two of the vertices of the Pedal Triangle do not lie on segments AB, BC, or AC)!
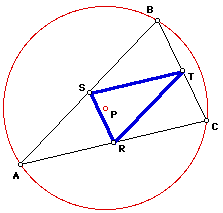
(2) When the Pedal Point P is the incenter of the given triangle ABC, the Pedal Triangle is the triangle whose circumcircle is the incircle of triangle ABC. This result occurs because P is the incenter, and so distances from P that are perpendicular to the sides of triangle ABC must be radii of circle P. Thus, R, S, and T must lie on circle P.
Notice that since the incircle always remains inside triangle ABC, all three vertices of the Pedal Triangle will always remain on the sides of triangle ABC in this situation as well.
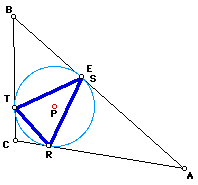
III. What are some interesting loci of vertices of a Pedal Triangle when the Pedal Point is a special point (not necessarily a center) of the given triangle?
The following loci are best seen as individual animated GSP sketches, rather than static images (although some images are included below.)
(1) When the Pedal Point P is the centroid of the given triangle ABC, at least two points of the Pedal Triangle appear to remain on triangle ABC at all times.
In particular, when point B is animated around circle C and point T of the pedal triangle is traced, it appears that the locus of T is a limacon. Download this GSP file to explore the situation and to determine when the locus will be a cardioid.
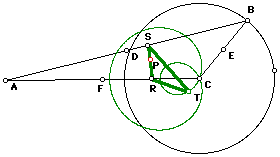
(2) When the Pedal Point P is the orthocenter of the given triangle ABC, the Pedal Triangle is the same as the Orthic Triangle. This result is not a big surprise, because the lines containing PT, PR, and PS are all perpendicular to the lines containing the sides of triangle ABC. So when AP, BP, and CP are all contained on the altitudes of triangle ABC, points R, S, and T are identical to the feet of the altitudes and thus triangle RST is the orthic triangle.
When point A is animated around an (arbitrary) circle D and points R and S are traced, the loci appear to be arcs of the same circle, and sometimes a complete circle. Download this GSP file to investigate when the loci of each point will be a complete circle. The locus of S is shown below (the image is not faulty--the locus is actually a major arc and not a full circle.)
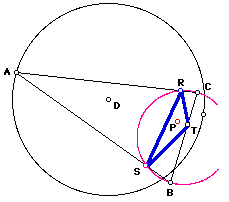
(3) When the Pedal Point P is the on a side of the given triangle ABC (P coincides with R below), interesting loci result from tracing point S as A is animated around circle D as shown. Notice that in some cases a sort of "sickle cell" shape appears, while in other cases, we see a what seems to be a limacon again! Download this GSP file to experiment with this situation.
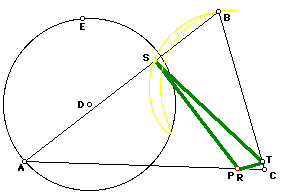
IV. What happens if a Pedal Point is animated around the incircle of the given triangle and the midpoints of the sides of the Pedal Triangle are traced? What if instead the excircle is used?
If Pedal Point P is animated around the incircle of triangle ABC (circle D below), the loci of all three midpoints (G, H, and I below) of the Pedal Triangle RST appear to be ellipses. Even more seems to be true: the axes of the ellipses fall on the angles bisectors of triangle ABC. In fact, even MORE is true, if one of the angles of triangle ABC is right.
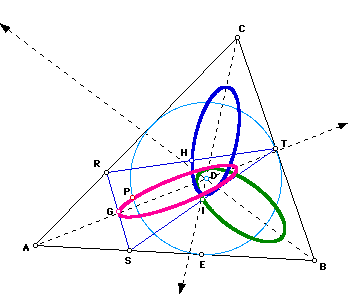
Download this GSP file to view the animation, to determine whether the major axes of the ellipses always lie on the angle bisectors, and to see what happens when triangle ABC becomes right.
If instead P is animated around the excircle, similar results occur. In the diagram below, K, L, and M are midpoints of the sides of Pedal Triangle RST and P will move around excircle E.
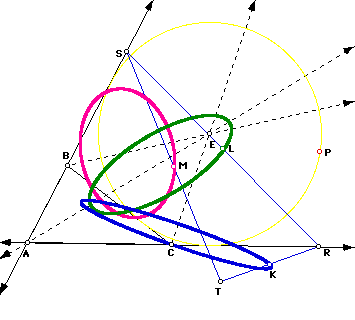
If you wish, download one more GSP file to explore. (Note that in the file, all three excircles are shown.)
Although I am far from any sort of explanation or proof of these conjectures, I have determined a few things:
That's all for now! Have fun exploring.