Essay 1. Distance in Minkowski and Cartesian Geometry

by Jongsuk Keum

Goal

We already know that what circles are in Cartesian Geometry. But circles in Minkowski geometry are remarkably different. Therefore, it's interesting for students to explore the d istance in Minkowski and Cartesian Geometry using GSP.

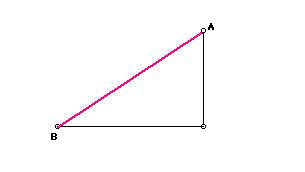
1. Distance in Cartesian Geometry

If point A has coordinates (x1,y1) and
point B has coordinates (x2,y2), the distance from A to B is

d(A,B) = sqrt[(x1-x2)2 + (y1-y2)2].

Hence, the distance in Cartesian geometry means the length of the hypotenuse of a right triangle.

2. Distance in Minkowski geometry.

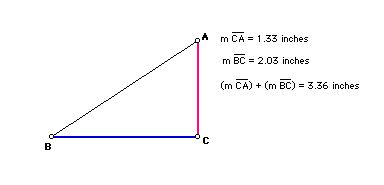
If point A has coordinates (x1,y1)
and point B has coordinates (x2,y2), the distance from A to B is

d(A,B) = |x1-x2| + |y1-y2|.

Hence the distance in Cartesian geometry means the sum of the length of base and height of a right triangle.

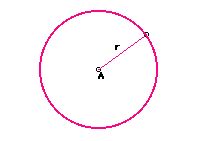
3. What are the circles in Cartesian geometry and Minkowski geometry?

a. Circle in Cartesian geometry with center A with a radius r

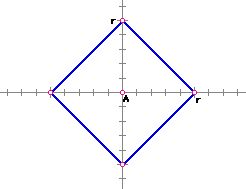
b. Circle in Cartesian geometry with center A with a radius r
Click here for construction

4. Equal distance set of A and B

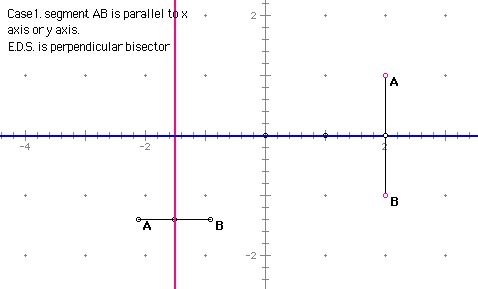
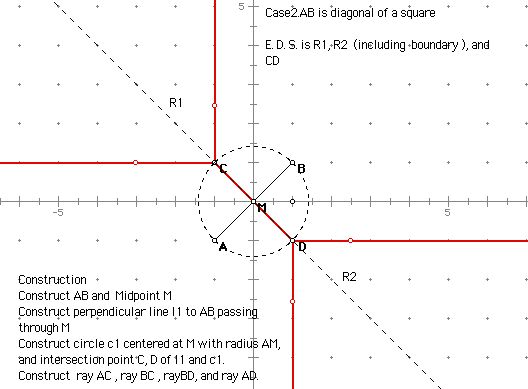
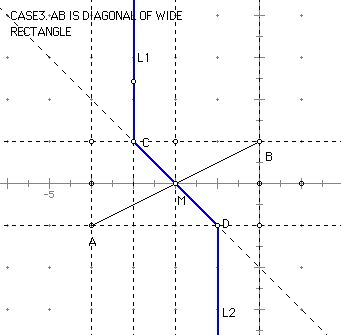
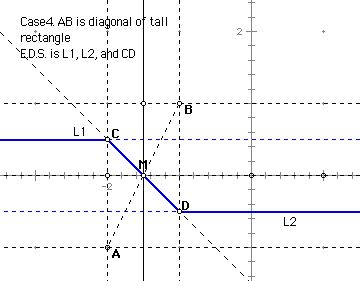
: the set of all points such that d(C,A) = d(C,B).

Return to Jongsuk's Homepage