Day 2 : Geometric Definitions of Translation, Rotation, Reflection, and Glide Reflection
by Jongsuk Keum

Day 2 : Geometric Definitions of Translation, Rotation, Reflection, and Glide Reflection
by Jongsuk Keum
| Type of Transformation | Defining Data |
| Translation | A vector, called the translation vector |
| Rotation | A point, called the center of rotation, & an angle, called the angle of rotation. |
| Reflection | A line, called the mirror of the reflection |
| Glide Reflection | A line, called the mirror, & a vector V, called the glide vector |
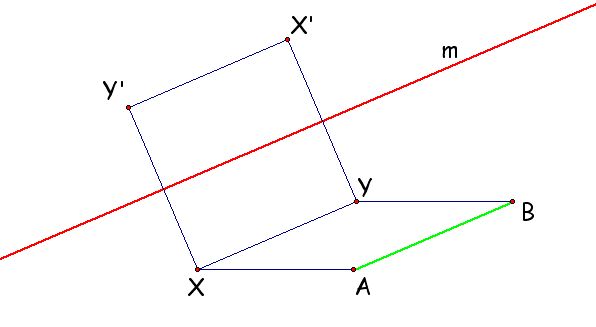
Let V be the vector from point A to point B.
If the point X lies on the line AB, then its image X'
also lies on AB, d(XX') =
d(AB), and X' is in the same direction from X as B is
from A. (This last condition
means that the union of the two rays ray(AB) and ray(XX')
is a ray, not the whole
line AB.)
If the point X does not lie on the line AB, then
X' is the point such that XX' is
parallel to AB and BX' is parallel to AX. In other words,
ABX'X is a parallelogram
.
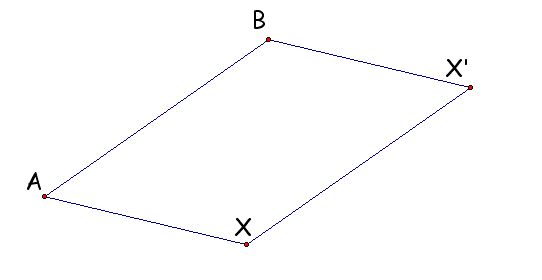
Geometric definition of rotation
If the point X is the center O, then the image X' is also O.
If the point X is not the center O, then the image X' is determined by
the properties that OX = OX' and the measure of the angle XOX' equals the
measure of the angle ABC.
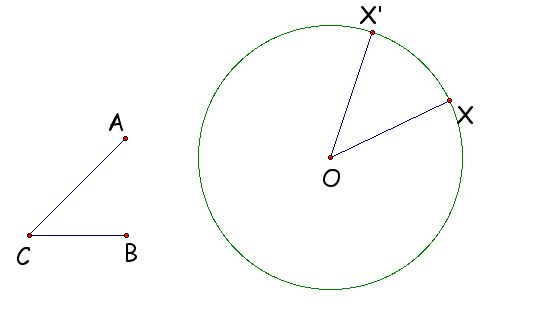
If the point X lies on the mirror line m, then its image point X' is equal to X.
If the point X does not lie on the line m, then its image point X' is determined by the property that the line XX' is perpendicular to the line m, and the distance from X' to m equals the distance from X to m. In other words, if P is the intersection point of the line XX' and the line m, then d(X'P) = d(XP). A concise way to say this is that the mirror line m is the perpendicular bisector of the segment XX'.
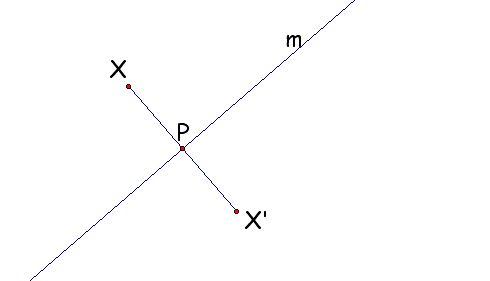
The defining data of glide reflection is a line m, called the mirror, and a vector V, called the glide vector. The vector V must be parallel to the line m. If we use an ordered pair of points A,B to determine the vector V, then the line AB must be parallel to the line m.
If the point X is on the mirror line m, then X' is just the translation of X by the vector V.
If the point X is not on the mirror line m, then X' is obtained from X by first translating by V and then reflecting across m. In other words, there is a point Y so that ABYX is a parallelogram and m is the perpendicular bisector of the segment X'Y.
(It follows that if Z is the reflection of X across m, then XYX'Z is a rectangle. Thus X' can also be obtained by first reflecting X across m and then translating by V.)