Day 5 : Products of Isometries
by Jongsuk Keum
Goal
Students explore the product of isometries using GSP, and
then prove the result.
The product of two reflections
We have three cases. Let m1 and m2 be the two
mirror lines.
Case1.If m1 = m2 then F1F2 = I.

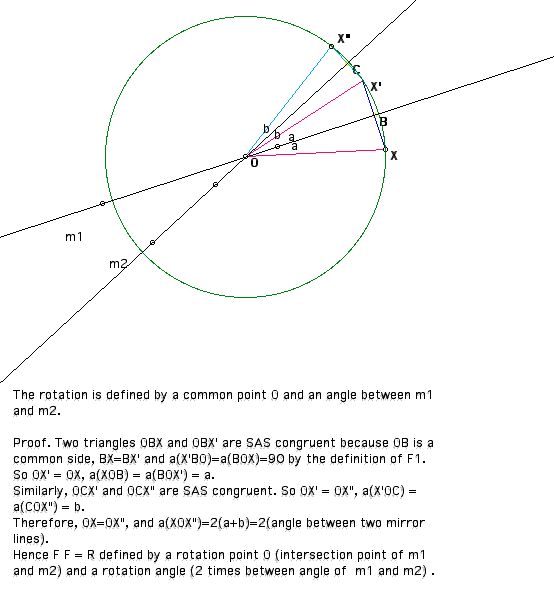
Case2. If m1 and m2 has a common point then F1F2 = Rotation.
the rotation is defined by the common point as a rotation center and 2
times angle between m1 and m2 as a rotation angle.
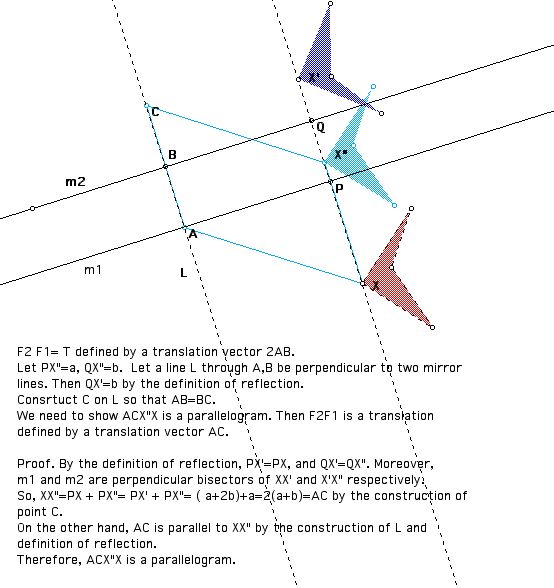
Case3. If m1 is parallel to m2 then F1F2 = Translation.
The translation is defined by a translation vector 2AB.
The product of a Reflection and a Translation
Case1. TF = G
Case2. TF1 = F2

Return to Jongsuk's Homepage





