Day 6 : The theory of Isometries and Coordinate Formulas for Isometries

by Jongsuk Keum

Goal

Students prove that 4 types of symmetries ( translation, rotation, reflection, and glide reflection ) are isometries using GSP. In addition, they check the following coordinate formulas for isometries using the GSP Calculate function. In each case apply the given isometry to a dynamic point P and check that, as you move the point P around, the x and y coordinates of the transformed point P' are related to the x and y coordinates of P by the given formula.
The following types of transformations are isometries:

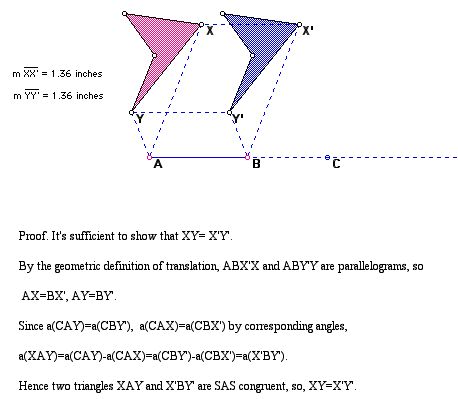
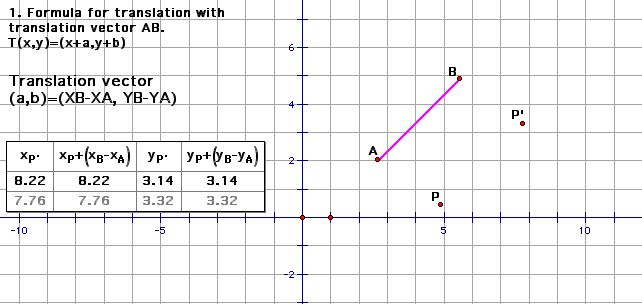
(a) translation

(b) rotation

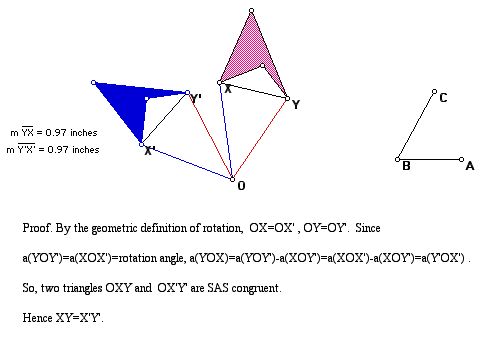
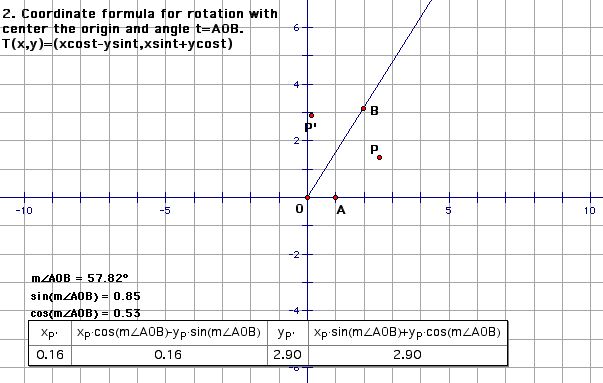
(c) reflection

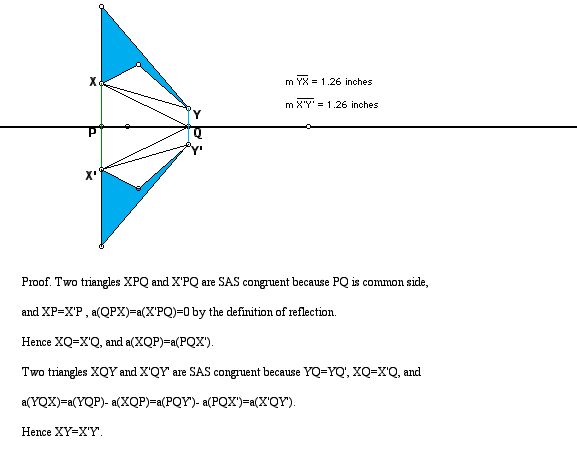
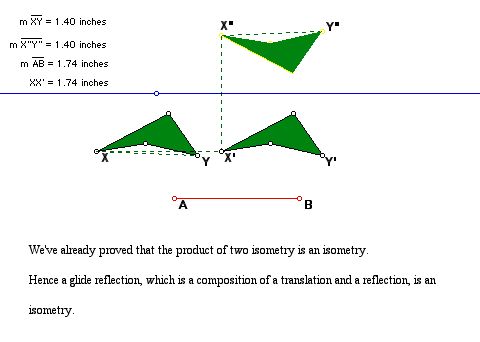
(d) glide reflection


1. Translation with vector (a,b).

T(x,y) = (x + a, y + b)

2. Rotation with center the origin and angle t. (t stands for theta.)

T(x,y) = (x cos t - y sin t, x sin t + y cos t)

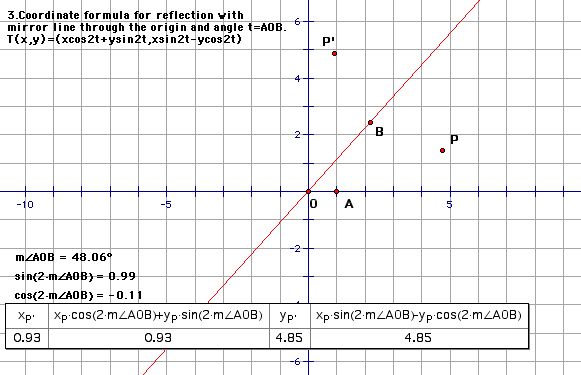
3. Reflection with mirror the line L through the origin such that the angle from the x-axis to L is t.

T(x,y) = (x cos 2t + y sin 2t, x sin 2t - y cos 2t)

4. Rotation with center (a,b) and angle t.

T(x,y) = ((x-a)cos t - (y-b)sin t + a, (x-a)sin t + (y-b)cos t + b)

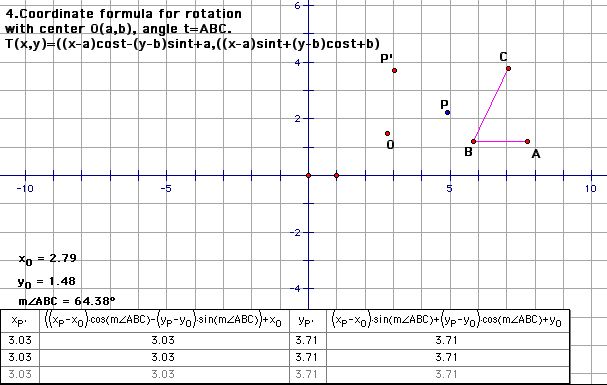
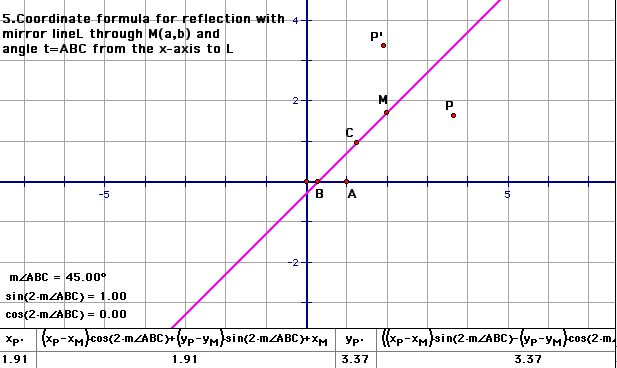
5. Reflection with mirror the line L through the point (a,b) such that the angle from the x-axis to L is t.

T(x,y) = ((x-a)cos 2t + (y-b)sin 2t + a, (x-a)sin 2t - (y-b)cos 2t + b)


Return to Jongsuk's Homepage