by Jongsuk Keum
Asymmetric pattern: The identity is the only symmetry of P.
Bilateral pattern: The only symmetries of
P are the identity and reflection with mirror L.
Example: A human's picture is almost bilateral symmetry.
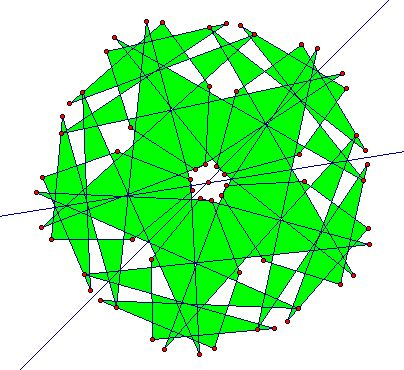
Radial pattern(Wheel pattern): The only possible
symmetries of P are the identity, rotations with center C, and reflections
with mirror through C.
Cn ( Cyclic group) and Dn( Dihedaral group) are
only possible infinite classes.
Strip pattern: There are seven types of strip patterns.
Wallpaper pattern: There are seventeen types of wallpaper patterns.
The set of symmetries of a pattern P is a group because the symmetries of a plane pattern P have the following four group axioms:
1. Identity: The identity isometry is a symmetry of P.
2. Product ( closed ): If the isometries S and T are symmetries of P, then their product isometry ST is a symmetry of P.
3. Inverse: If the isometry S is a symmetry of P, then the inverse isometry S-1 is a symmetry of P.
4. Associativity: If the isometries S, T, U are symmetries of P, then (ST)U = S(TU).
| R0 | R1 | R2 | R3 | R4 | F0 | F1 | F2 | F3 | F4 | |
| R0 | R0 | R1 | R2 | R3 | R4 | F0 | F1 | F2 | F3 | F4 |
| R1 | R1 | R2 | R3 | R4 | R0 | F1 | F2 | F3 | F4 | F0 |
| R2 | R2 | R3 | R4 | R0 | R1 | F2 | F3 | F4 | F0 | F1 |
| R3 | R3 | R4 | R0 | R1 | R2 | F3 | F4 | F0 | F1 | F2 |
| R4 | R4 | R0 | R1 | R2 | R3 | F4 | F0 | F1 | F2 | F3 |
| F0 | F0 | F4 | F3 | F2 | F1 | R0 | R4 | R3 | R2 | R1 |
| F1 | F1 | F0 | F4 | F3 | F2 | R1 | R0 | R4 | R3 | R2 |
| F2 | F2 | F1 | F0 | F4 | F3 | R2 | R1 | R0 | R4 | R3 |
| F3 | F3 | F2 | F1 | F0 | F4 | R3 | R2 | R1 | R0 | R4 |
| F4 | F4 | F3 | F2 | F1 | F0 | R4 | R3 | R2 | R1 | R0 |
D5 has 10 symmetries, i.e., 5 reflections and 5 rotations;
R0 -------- rotation by 0
R1 -------- rotation by 72
R2 -------- rotation by 144
R3 -------- rotation by 216
R4 -------- rotation by 288
F0 -------- reflection mirror 0
F1 -------- reflection mirror 36
F2 -------- reflection mirror 72
F3 -------- reflection mirror 108
F4 -------- reflection mirror 144