

In doing explorations in mathematics classes the spreadsheet proves to be quite a utilitarian tool. An aspect of these applications that makes them so useful is that a spreadsheet may be adapted to many different explorations, presentations, and simulations in mathematics. There are spreadsheets available on almost any platform so most if not all students should have access to these tools. An essential feature is the ability to make graphs and charts from the matrix of data. It also proves helpful if the program has the capability to add a trendline or curve of best fit to the graphed data. This feature allows students to relate a mathematical equation to a set of real world data.
For this write up I have chosen to present my findings about data provided us from the lumber industry. (Here the tree hugger in me, comes out.) As shown in the table below, the number of years that a tree has been growing plays an important part in the amount of board feet that may be harvested once the tree has been murdered (I mean cut down). Below see the chart that was created using information from the lumber industry. Click here to access an EXCEL file that contains this data. Note: I do not know what type of tree this refers to and as trees grow at different rates, certainly this does not apply to all species of our bark covered friends.
| Age of Tree | 100s of Board Feet |
| 20 | 1 |
| 40 | 6 |
| 60 | |
| 80 | 33 |
| 100 | 56 |
| 120 | 88 |
| 140 | |
| 160 | 182 |
| 180 | |
| 200 | 320 |
Having the desire to fill in the blanks in the table above as well as determine the number of board feet produced by a tree that has lived some other number of years, I used EXCEL to produce a graph of these points. Choosing a chart that forms a scatterplot, I was able to form an opinion of what type of function may best describe the data in question. Viewing the created graph (click here to access the file from which the diagram was created) I determined that raising the lifetime of the tree to a particular exponent and multiplying by some small number would produce a graph that resembled the scatterplot of the tree data shown below.
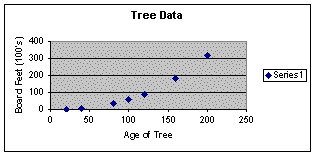
I next used EXCEL to create a line of best fit so that I could decide if my assumption was correct. This program allows the user to choose from several types of functions in order to determine which fits the data most closely. I chose a power function and EXCEL fit one to my data. See the graph below.
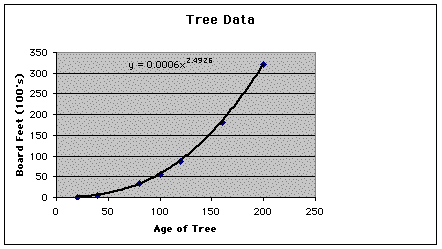
Notice that the curve does not contain each point, but is simply an approximation of a function that comes as close as possible to each data point. The function used by EXCEL is shown at the top of the graph. I used the spreadsheet to determine the exact value given by the function for each of the ages of the tree. The third column in the chart below shows the exact values.
| Age of Tree | 100s of Board Feet | .0006x^2.4926 |
| 20 | 1 | 1.04978078093774 |
| 40 | 6 | 5.90807479520481 |
| 60 | 16.2319634865331 | |
| 80 | 33 | 33.2501303315481 |
| 100 | 56 | 57.9897518588528 |
| 120 | 88 | 91.3520766362346 |
| 140 | 134.149788442423 | |
| 160 | 182 | 187.128837292692 |
| 180 | 250.982532174753 | |
| 200 | 320 | 326.361272332902 |
Since the numbers towards the bottom of the chart were poor
approximations of the actual values given, I chose to use the
spreadsheet in order to check other related functions and see
if it were possible to find a function that approximated the data
more closely. Click
here to access the spreadsheet I created for this purpose.
In this file at the top of each column is the formula used to
determine the values that follow. In my opinion no perfect solution
exists. If a teacher uses an example such as this in class, it
lends itself very nicely to valuable mathematical discussion from
the students of the class. Feel free, once opening the file,
to attempt to find functions that fit the data more closely.
In order to determine the values that have been excluded from
the table I choose to use the function f(x)= 0.000596*(x^2.49)
as this choice came nearest to the actual data in my opinion.
Evaluating at x = 60, 140, and 180, I find that trees these ages
would produce 15.95, 131.55, and 245.97 hundreds of board feet
of lumber respectively (as may be seen below).
| Age of Tree | 100's of Board Feet | 0.000596*(x^2.49) |
| 20 | 1 | 1.03469166099492 |
| 40 | 6 | 5.81266960501264 |
| 60 | 15.9530186604782 | |
| 80 | 33 | 32.654296164472 |
| 100 | 56 | 56.9175581268777 |
| 120 | 88 | 89.6205412410452 |
| 140 | 131.554306216595 | |
| 160 | 182 | 183.444635676095 |
| 180 | 245.965840815659 | |
| 200 | 320 | 319.750291403251 |
In order to find how many hundreds of board feet would be produced
by trees of different ages, one may use the link to the spreadsheet
above (Click here to jump to the
link for this spreadsheet) and simply change an already
existing value or add a new one to the end of the column.
I believe it would be interesting to try to determine a tree's
ideal age when the lumber industry should harvest their product.
Of course, more information than is given here would be needed
in order to find this particular value. Also, one's personal
opinions would play a role in this investigation as well. I for
one see this as a reason to allow trees to live longer lives.
By harvesting only older trees the lumber companies would be
able to yield more board feet by cutting down fewer trees. Of
course, my bias that the fewer trees cut the better off we will
be plays a role in this comment. Perhaps this also may lead to
the end of the disastrous practice known as clear cutting.