,
and its graph. Then, I will replace the x in the equation with
other values for the variable and determine what this change does
to the graph. This exploration will lead to a discussion of how
a graph changes based on the adjustments made to the equation.
Let's begin by looking at the graph of the equation that will start this discussion.
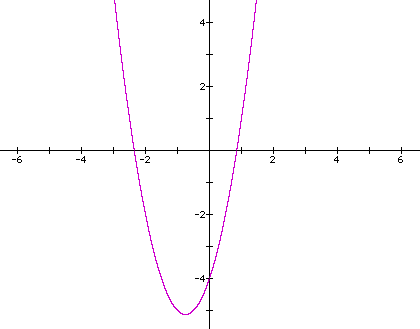
We see that the quadratic equation,,
yields the graph of a parabola as we would expect. Using the abilites
of the graphing calculator program we can see that the roots of
this equation are at x = -2.35 and x = 0.85. Also, the program
allows one to find the minimum point on this graph, the vertex
of the parabola. Here it is at (-.75 , -5.125). These are helpful
points to know as will be seen later in this investigation.
Now by substituting x-4 in for each x we arrive at a new equation. The diagram below compares the graph of the original quadratic equation to this new equation.
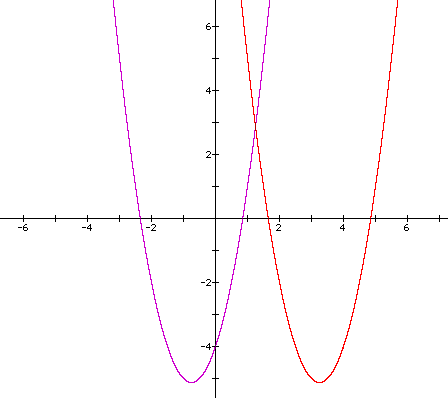
The red parabola in the above diagram is the graph of the new equation. It seems to be the same as the original (purple) equation but for the fact that it has been shifted to the right. The next question is how far to the right did it move and did it move along the y-axis at all. By comparing the roots and the vertex of the new equation to the original we can determine the distance the graph shifted. The vertex of the new parabola is (3.25 , -5.125). This value allows one to surmise that the graph as not moved vertically, but it has moved to the right 4 units. Comparing the roots of the new equation will help to prove this hypothesis. The red curve has roots at x = 1.65 and x = 4.85. Certainly this information tells us that the graph has moved right four units. So one may conclude that changing the variable x to x-4 will move the graph four units to the right. What would happen if we replaced x with x-7? View a graph. Or if we replaced x with x+ 16? View a graph.
Now I would like to not only be able to move a given graph left or right, but also move it up or down. For example, would it be possible to make the majority of the original graph reside in the second quadrant? Here I speak of the majority of the graph because if one moves far enough towards infinity along the y-axis, we are sure to see the parabola cross this axis and move into quadrant I of the coordinate plane. Certainly the graph must move left, but it also needs to shift up the vertical axis. See the diagram below for one example.
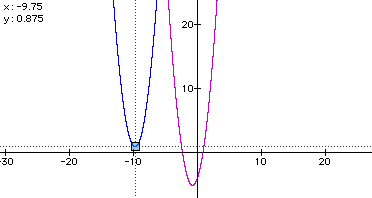
Here I have changed the original by substituting x + 9 for each x, and I have also added 6 on the end of the first equation. I could have written this equation in simplified form, but then it would make the discussion of the movement of the graph not nearly as clear. The top left corner of the diagram shows the minimum point of this new parabola. The vertex is at (-9.75 , 0.875). Comparing this new point to the vertex of the original parabola at (-.75 , -5.125), one may see that the graph has shifted nine units to the left (as one may expect from the earlier portion of this discussion) and moved six units up. This vertical shift is directly related to adding six to the end of the equation. To see other examples click here.
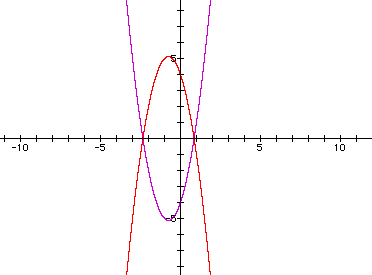
In each of the parabolas that we have viewed thus far the vertex has been a minimum and the shape has been concave up. We will know look at what is necessary to make the vertex a maximum and thus allow the parabola to be concave down. It seems obvious that placing a negative in front of the entire equation will reflect the graph over the x- axis since all positive y values will become negative and all negative y values will become positive. The graph may be seen below.
What must happen in order to make the two parabolas
share the same vertex? In order to discuss this it is necessary
for us to know that an equation of the form 
is
a parabola whose vertex is at the point (h,k) and a is a constant.
By completing the square, we may write 
in
the above form. The new equation is 
.
Here we see that the vertex of this parabola is ( -0.75 , -5.125
). To make this parabola become concave down and keep the same
vertex, simply make the constant, a, the opposite sign. So 2 becomes
-2 and we get the equation 
.
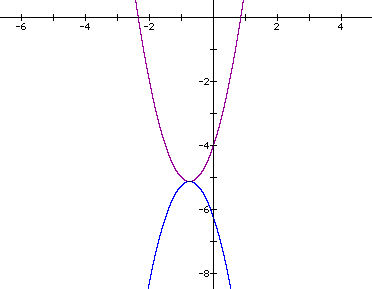
Below is a diagram showing the graphs. Notice the purple and red
graphs coincide showing us that the two equations are equivalent.
In conclusion, this assignment allows for the investigation of several shifts of a quadratic equation's graph. In addition to being able to slide a graph without it changing shape, it is also possible to adjust the equation to make the given parabola become thinner or wider. Also, we could change the equation to make the parabola open left or right rather than simply up or down. Of course, the equation would no longer be a function, but all the same we can make the graph look however we want it by making a few changes to the equation.