

In the fourth investigation of this course, I chose to prove that the medians of a triangle were concurrent. Along with this proof came the corollary that the distance from this point of concurrency to the midpoint of the side of the triangle is one third of the length of the median itself. Having this knowledge drew me to the intriguing problem of creating a triangle if I was given its medians. As it turns out the corollary that was proven in investigation four is pivotal to this construction.
Begin with the given lengths of the medians. Note the differing colors as this coding will enable the reader to better follow the discussion.
To begin the construction I made a triangle with lengths that were the same as the given medians. This is quite an easy construction. Simply choose one segment and construct circles at its endpoints with radii equal to the other lengths of the two unused segments. The point where these two circles intersect is the third point of the triangle. Below is the triangle with which I will continue this investigation.
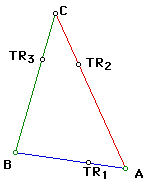
The colors remain consistent with the given segments. Also on this triangle are points which divide the segments at one third of their length. I chose to do this since the medians meet at a point which is one third of their total length.
Now I wish to position two of the given segments parallel to their respective original side of the triangle ABC. The important thing is that the points dividing the medians into one third and two thirds must meet. Also, the portion that is a third of one median must lie between the portions that are two thirds of the other medians. This statement tells us that if I simply translate BA to lie at PN (see diagram below), my construction will not work. I was forced to reflect BA around the dividing point TR1. Likewise, AC was not simply translated, but reflected about TR2 and positioned accordingly. Of course, to construct this figure using The Geometer's Sketchpad (GSP), I did not just grab, flip and drag the segments. Instead I had to draw circles centered at TR3 with radii that were equivalent to the appropriate parts of the given medians. To construct NP, draw a line parallel to AB through TR3. Create segments ATR1 and BTR1. Construct a circle centered at TR3 with radius ATR1 and construct a circle centered at TR3 with radius BTR1. Choose the proper intersection points between the circles and the constructed parallel line and connect P and N to form the median of the triangle we wish to construct. The same process is followed to construct ML using side CA and point TR2.
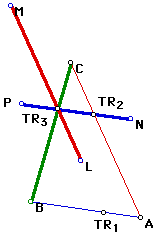
Having completed this most difficult portion of the construction, I simply connect M, N, and B to form the desired triangle which is seen below.
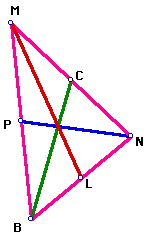
I note here that the endpoints of the images of the given medians, P and L, are the midpoints of MB and NB respectively as they should be. We may use GSP to check that this assumption is correct for this case.
To access the GSP sketch I used to create this page, click here.