

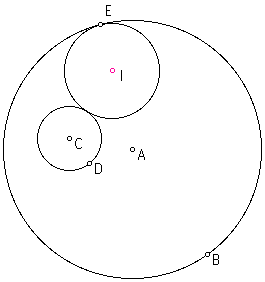
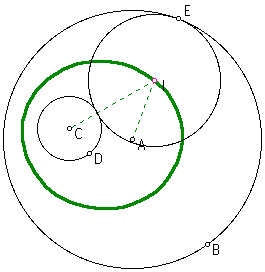
One distinguishing feature between cases is the location of the point used to create the tangent circle, that is the point on the given circle where the constructed circle is tangent. Here in case one the point is E on the circle centered at A and passing through B. The circle centered at C is the second given circle and I is the tangent circle.
The second case also chooses a point on the large circle tangent to the circle we wish to construct. In this case however, the tangent circle will contain the smaller of the given circles. See below to visualize this case.
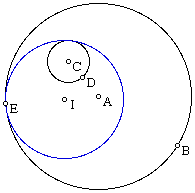
Here the circle centered at I is tangent to both the large circle centered at A and the smaller circle it contains, centered at C.
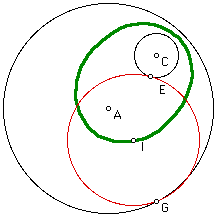
The third case is identical to case one with the exception that the point used to generate the construction was the tangent point on the smaller circle. See below.
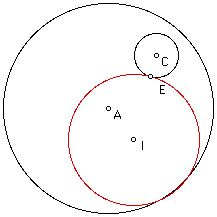
Note the only difference in this case and the first is that point E is the tangent point on the smaller circle centered at C.
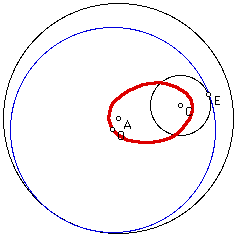
The final case is the same as the second case with the only difference being that the construction began with a point on the smaller circle as a point of tangency. Below is an image to illustrate this statement.
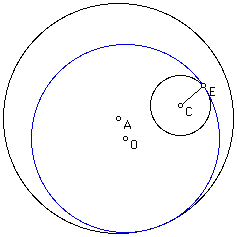
Here note that the point of tangency, E, is on the smaller of the given circles.
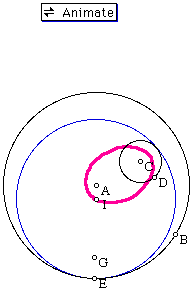
Here the curious reader may be questioning if the constructions shown would hold true for any point on the given circle. Below are a series of links that connect to Geometer's Sketchpad (GSP) files that will allow the reader to determine if in fact the circle shown is tangent at all points. One may either double click the animate button once the file is downloaded to allow the point of tangency to move around the circle on which it is a point, or simply select the point and move it around the circle with the mouse.
Link to:
Also, one may desire to be able to create similar constructions to investigate some of the interesting aspects of this problem on his own. As a device to aid this person I include below the Geometer's Sketchpad scripts used to create each of the different cases.
Download the script to create:
Here the abilities of The Geometer's Sketchpad that allow for investigation, demonstration, and exploration help to make it a remarkable tool for helping learners develop statements to be proved and for the construction of new relationships. The set of circles tangent to two given circles, as discussed here, is a very rich problem environment. GSP helps individuals to visualize and demonstrate; that it allows for a means to pose a considerable array of related problems and investigations.
One interesting aspect of this construction is the loci of the centers of the tangent circles for each case. Each case shows us that the centers of the different circles tangent to the others form an ellipse such that the centers of the given circles are the ellipse's foci. Here is an instance where the abilities of GSP are greatly appreciated by learners. By allowing the point of tangency to run about the circle it is a point on and having GSP create the locus of the centers, we clearly see the ellipse for each case. Choose any case above to experiment for yourself or look below for some examples.
The next variation I would choose to discuss here is the case where the two given circles intersect or are separate from one another. In these situations the loci of the tangent circles tend to behave a bit differently. As a note to the reader I state here that in constructing the circles for the rest of these investigations I created disjoint circles and then moved them to meet the conditions necessary. When I created circles that intersected as intersecting, I was unable to separate the two to look at those particular cases.
Case One with intersecting circles:
Here it is shown that the locus of the centers of the tangent circles forms an ellipse when the given circles are intersecting. Click here to access the GSP file which created the image below.
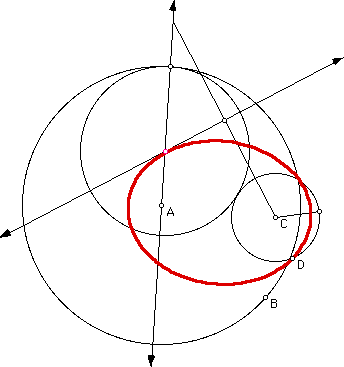
Case One with Disjoint Circles:
Here we see the first instance where the loci of the tangent circles do not make an ellipse, but rather sweep out an hyperbola. Click here to download the GSP file that shows this characteristic. Note here that at a point the tangent circle becomes a line (which is truly just a circle with infinite radius, isn't that correct Dr. Wilson).
Case Two with Intersecting Circles:
Again the loci of the centers of the tangent circles form an hyperbola. It is worth the reader's time to click here so as to access the file I created to explore this situation. Once the GSP file is downloaded, double click the animate button and watch the tangent circle become interior to the smaller given circle as it passes point K and then return to its original position as it passes point J. It is worthy of noting that the circle remains tangent to both given circles at all times. Really click the link and see for yourself.
Case Two with Disjoint Circles:
Here again the loci of the tangent circle's centers form an hyperbola and at one point the circle "breaks into a line" and then becomes a circle again. Clicking here downloads the GSP file that illustrates this statement.
For cases three and four if the circles intersect or are disjoint, then the tangent circle does not always exist according to my scripts or in some instances the circle exists, but is not tangent to both given circles. To access those files select one of the following links.
Case four, intersecting circles
Case three, intersecting circles
As not all cases of the above investigation yielded interesting effects, but some were quite remarkable, next I look at the loci of the midpoint of the isosceles triangle which is integral in determining the center of the tangent circle. To read the discussion of the construction of this triangle link to the Assignment 7 page of EMAT 6680. The sketches below and the links to GSP files relate to the loci of the midpoints of the base of the ever important isosceles triangle in this construction.
In case one the trace of the midpoint, M, is shown to be a circle, click here for access to the GSP file.
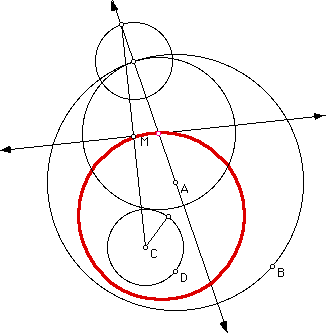
Case two shows the loci of M are also of the form of a circle. Click here to download the GSP file which created the image below.
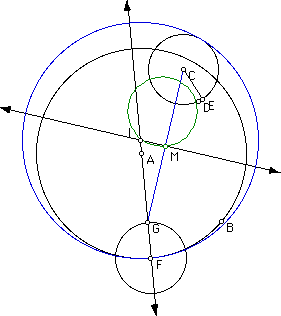
Here in case three, we see the first instance where the trace of the midpoint, M, does not appear to be a circle. Click here to access GSP and determine for yourself if the loci form a circle.
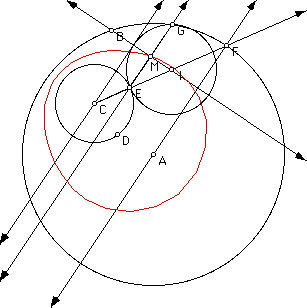
In case four I have shown the loci of the midpoints of two isosceles triangles. One is quite interesting while the other is similar to that seen in case three. Click here to access the GSP file used to create the image below and experiment for yourself.
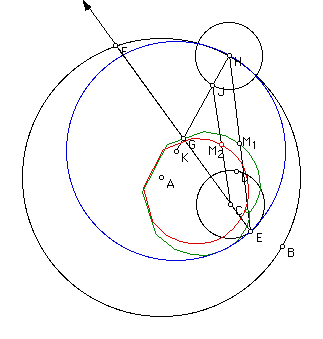
In the diagram above M1 is the midpoint that creates the loci with the loop in it. Quite intriguing. Would it occur in case three? Check the link for case three and determine an answer.