

This investigation revolves around the altitudes of triangle. The altitudes of any given triangle will always intersect in one given point. To see a GSP sketch that illustrates this fact, click here. The point where the altitudes meet is called the orthocenter of the triangle. By connecting this point, call it H, to each of the vertices of the triangle, we obtain three new triangles. See the diagram below. To view the GSP file which constructed the figure, click here.
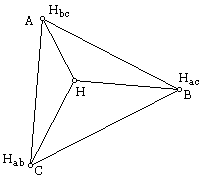
In the above figure Hab is the orthocenter of triangle HAB, Hbc is the orthocenter of triangle HBC and Hac is the orthocenter of triangle HAC. It is interesting to note that the orthocenters of any of the orthic triangles fall on the vertex of the original triangle that is not a point in the orthic triangle in question. For instance Hab is the orthocenter of triangle HAB and Hab is the same point as C in the original triangle. Certainly one could construct a proof of this fact. I choose to look at another, more interesting characteristic in my opinion.
When we draw the circumcircles of each of the four triangles, the original and its three orthic triangles, the circles appear to be the same. See below for a diagram or click here to access the GSP file used to create the image.

Since the circles appeared to be congruent, I used GSP to find their areas. The areas of the four circles were all equivalent, I started to try to find a proof of this fact. To simplify things I decided to consider two of the circumcircles. I wish to use the circle about triangle ABC and the circle about triangle HAC. Proving these two congruent will lead to the fact that all four circumcircles must be congruent, as the reasoning applied to the circle about triangle HAC would easily fit for the circles about the other orthic triangles.
The diagram below will aid this proof. If you wish to access a GSP sketch, click here.
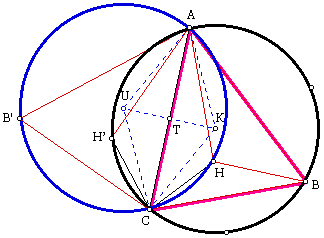
To begin note that AC is a chord common to both circles. The diagram contains a couple of constructions. One is a reflection of triangle AHC across the segment AC. Also I have reflected triangle ABC across the segment AC. This last triangle, AB'C is not necessary for the proof, but it is going to play a part in a discussion following the proof, thus I included it. It is also necessary to note that K is the center of the circle which circumscribes ABC and U is the center of the circle which circumscribes AHC. From this point I will refer to the circles by these centers. By proving the radii of the two circles equal, I will have proven that the two triangles must be congruent. With this in mind I begin.
First, it is essential to realize that the reflection of H, namely H', is a point on circle K. I do not have a proof to show why this must be true, but reflecting the orthocenter across any segment of the triangle gives an image that is a point on the circumcircle.
Angle AH'C is an inscribed angle of circle K which subtends the same chord as the central angle AKC. So the measure of angle AKC is twice that of angle AH'C. Likewise I know that angle AUC is twice the measure of angle AHC. This relation comes directly from the fact that angle AHC is an inscribed angle of circle U and subtends the same chord as the central angle AUC. Since angle AHC is the same measure as AH'C (the latter is the reflected image of the former), I know that AUC is equivalent to AKC. Because triangles AUC and AKC are isosceles (UA and UC, AK and KC are radii of circles U and K, respectively) and angle AUC is equivalent to angle AKC, then the base angles of the triangles must also be congruent. Thus angle UCA = angle UAC = angle KAC = angle KCA. Recalling the triangles UCA and KCA share side AC, I know the triangles are congruent due to the ASA triangle congruency axiom. Therefore, the corresponding parts of the triangles must be congruent. Thus UA = AK = KC = CU. This fact tells me the radii of circle K are equal to the radii of circle U and finally that the circles are congruent. As stated above this strategy of proof may easily be applied to show the other circumcircles congruent to circle K and thus that all four are congruent.
I believe this construction (a triangle, its orthic triangles and the circumcircles of the four) leads to other interesting investigations. For example, why are the reflections of the orthocenter, the vertex of the triangle which is opposite the line of reflection (B in the above figure), and the reflection of this point (B' in the previous diagram) all collinear.
Also, connecting two circle centers (if the circles intersect) with a segment, we get a segment that is the perpendicular bisector of the chord shared by the two circles. An illustration of this can be seen in the above diagram. There UK is the perpendicular bisector of AC. These facts follow directly from the fact that any point which is the same distance from the two endpoints of a segment is a point on the perpendicular bisector of said segment. Even more powerful is the fact that this holds true for any size circles, they need not be congruent.
What else can be discovered using a diagram such as these shown here?