

This investigation concerns a given triangle and the pedal triangle, which relates to this given figure. A pedal triangle is formed by constructing perpendiculars to the sides of the original triangle (the sides of the original triangle may be extended if necessary) and locating the three points that are the intersections of the perpendiculars with the original sides (or their extensions). In the diagram below triangle RST is the Pedal Triangle for Pedal Point P given the original triangle ABC. To access the GSP document used to create the diagram, click here. This document will allow movement of both the pedal point and the vertices of the original triangle to enable one to view the changes in the pedal triangle for particular locations of the pedal point as well as the vertices of the triangle.
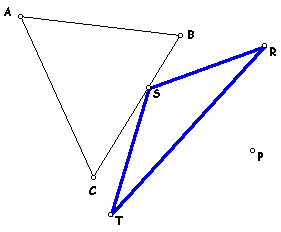
One may assume that choosing different points as the pedal point may illustrate some interesting relationships between the original triangle and the pedal triangle. I chose to let the pedal point be situated at each of the four basic triangle centers (orthocenter, circumcenter, incenter, and centroid). My investigations lead to the conclusion that the pedal point being located at the circumcenter gives consistent relations between the original and pedal triangles.
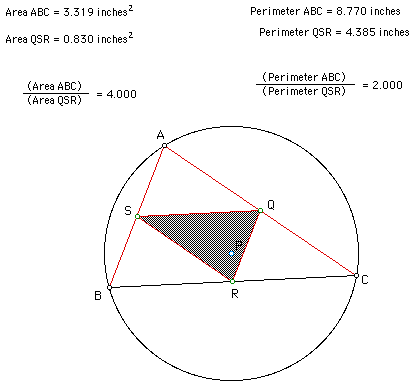
As shown by the GSP sketch above the ratio of the area of the
original triangle, ABC, to the pedal triangle, QSR, is four to
one. Also, the ratio of their perimeters is two to one. In order
to access the Geometer's Sketchpad document that created the above
diagram, click here.
Once one has downloaded the document, it may be easily seen that
moving any vertex of the triangle preserves the ratios described
above.
Due to the fact that the pedal point being located at the circumcenter
of the original triangle yielded some interesting relationships,
I am led to consider the pedal point as a point on the circumcircle
of the given triangle. As may be seen in the diagram below, if
the pedal point is on the circumcircle, then the pedal triangle
is degenerate, that is it makes a straight line. Click
here so that the document used to create the figure below
may be viewed. Once you have accessed the document, by double
clicking the button labeled animate, one may see that for all
points on the circumcircle the pedal triangle is always degenerate.
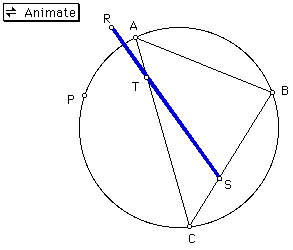
These special locations of the pedal point, where the pedal triangle
is degenerate, are the only such points I was able to determine.
When the vertices of the pedal triangle are collinear, they are
said to form the Simson line. Although this is a misnomer and
an individual named Wallace is credited with determining this
fact, the naming has remained attributed to Simson.
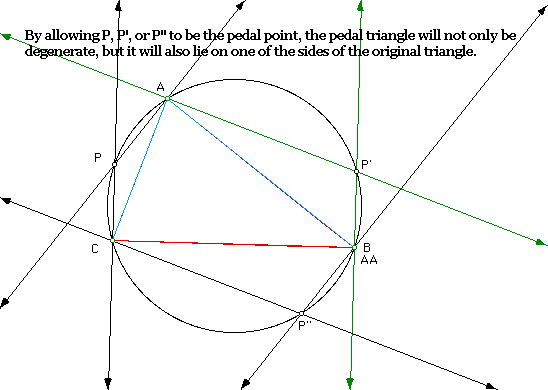
A further investigation that may prove interesting is to attempt
to find a point so that the Simson line coincides with one segment
of the original triangle. By finding the intersection of the
circumcircle and the perpendicular to a side of the triangle through
a vertex at the end of this side, one finds a point where the
pedal triangle is not only degenerate, but the Simson line lies
on a side of the original triangle. For an example, see below.
To access a file that shows all the points where this occurs,
click here.
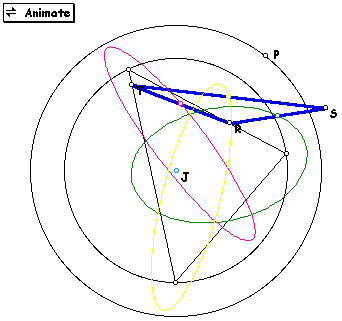
Another interesting characteristic of pedal triangles may be seen
if the midpoints of the pedal triangle are traced as the pedal
point is animated about different medium. For example, if one
allows the pedal point to revolve about a circle, the midpoints
sweep out ellipses as is seen in the diagram below. Click
here to access the GSP file used to create the diagram.
In order to view the ellipses as they are being created, use the
link to open the file that created the diagram below and double
click the animate button. While this GSP file is open, it is quite
interesting to adjust the figure and view how the loci are affected.
What would you expect the locus of the midpoints of the pedal
triangle to be if the pedal point moves around the circumcircle
of the original triangle? Click
here to view a GSP file that will allow you to find the
answer to this question.
Concluding, the relationship between a triangle and its various pedal triangles is clearly rich with possibilities for investigation.