
| This is the write-up of Assignment #6 |
Brian R. Lawler
|
| EMAT 6680 |
12/12/00
|
The Problem
| 3. Given line segments j, k, and m. If these are the medians of the triangle, construct the triangle. | 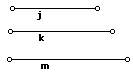 |
Process to Solve
I did not take careful notes on the misguided attempts and incorrect paths I pursued, but will be able to refer to a few of them along the way as I reconstruct the majority of my successes towards solving this problem.
| Early on, I decided I wanted to place the segments onto a GSP page in a manner that would allow the user to change the size of the segment, but restrict this resizing along a horizontal line. This was really only to keep the results neat. I suppose I also wanted to learn how to do this. To accomplish this wasn't difficult. The key was not to begin with the segments constructed, but to begin with only a point (3 points), then create lines through them. After selecting a point on the line, I could hide the line and construct a segment connecting the points. Now as this new point was moved around, it was tied to the parent hidden line. | 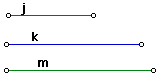 |
Another phase of solving this problem was to learn how to construct a new segment with the exact length of my starting segment. I constructed a new location on the sketchpad and built a circle with this as it's center and a radius of segment j. Then I selected a random point on the circle in order to locate the other end of my newly created segment, from radius to this point. This became my replicate of segment j. One end of this segment identified one vertex of the triangle I needed to construct. I named this point A.
Next I had to copy the other segments over here, but specifically had to arrange them in a manner that would create a triangle with these segments as it's medians. My first thought was to locate a point 2/3 along the first translated segment and force the other two segments through that point (the centroid of the triangle I am trying to construct.) I was thinking this because I knew the medians of a triangle are concurrent at a point that divides each segment into 2/3 and 1/3. To accomplish this, I trisected the translated segment j to locate this point of concurrence. Then I trisected the original segments k and m. Now I could redraw these segments through the centroid. Before progressing much further, I knew that is would be a problem. These new constructions would just flop around and NOT identify the 2 additional vertices of the specific triangle I needed.
| To rethink my approach, My next task was to just create a triangle of these medians. This was simple a matter of drawing a circle with radius k at one endpoint and one of radius m at the other. The point of intersection marked the third vertex of this median triangle. |
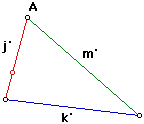 |
|
| Next I sketched a line parallel to m' through the centroid. Now I saw that I needed to place a copy of segment m' onto this parallel line. The 1/3 point of this copied segment had to lie directly on the centroid. I accomplished this by trisecting m', then drawing several circles along the parallel line and identifying endpoints of the desired segment, labeled m''. Most importantly is that I have now identified a second vertex of the final triangle, labeled B. |
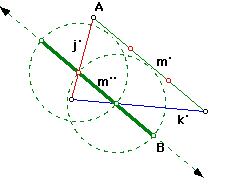 |
|
| I more or less completed the same construction from line k' to locate C. | And the final step was to connect the new vertices and hide the remaining construction steps. |
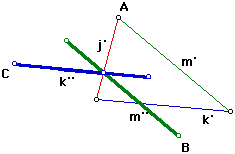 |
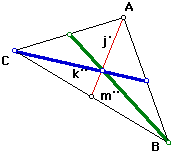 |
Conclusions
|
The solution to this problem really lies in the work to complete the construction of the triangle at right. (Please note, the orientation of the labeling in the picture at the right has changed from the process section above.) The lengths of the medians were maintained via the constructions. An assumption I made along the way was once this triangle was formed, it's medians must be parallel to a triangle constructed of the medians. I am uncertain to what extent that is a property inherent in the geometrical relationships or if it was merely a handy method to for constructing. I am choosing to end my work on this problem and this write-up now, so if anyone who reads this has some insight into this question, please e-mail me your thoughts.
Click here to interact with the completed sketch in Geometer's Sketchpad. Click here to download a script to generate the result. |
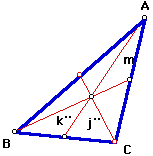 |
Reflections
I am quite proud of this result. It turned out to be a rather difficult construction that I was able to complete mostly on my own. Thank you to Dr. Wilson for the tip to generate a triangle of the medians and build off of that. Also, I did not write this up immediately after completing the GSP work and found I had to rework much of the problem to remember how! If you decide to look at the work in GSP, select "Show All Hidden" in the "Display" menu to get a sense of the work involved.
Some additional problems I partially investigated
1. Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove whatever you find.
2. If the original triangle is equilateral, then the triangle of medians is equilateral. Will an isosceles original triangle generate and isosceles triangle of medians? Will a right triangle always generate a right triangle of medians? What if the medians triangle is a right triangle? Under what conditions will the original triangle and the medians triangle both be right triangles?
4. A 4 by 4 picture hangs on a wall such that its bottom edge is 2 ft above your eye level. How far back from the picture should you stand, directly in front of the picture, in order to view the picture under the maximum angle?
|
6. Given three points A, B, and C. Draw a line intersecting AC in the point X and BC in the point Y such that AX = XY = YB
|
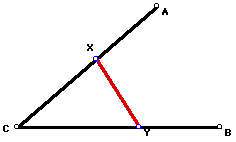 |
|
7. Construct the common tangents to two given circles. Make a script. Test it for all the different cases.
 |
Comments? Questions? e-mail me at blawler@coe.uga.edu |
| Last revised: December 28, 2000 |
|