
| This is the write-up of Assignment #9 |
Brian R. Lawler
|
| EMAT 6680 |
01/02/01
|
|
I.
|
See the Definition and Construction of a Pedal Triangle |
| Exploring conditions of the Pedal Triangle | |
| Considering various loci and traces |
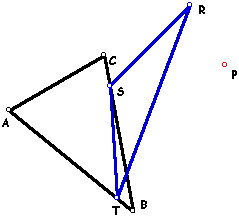
| 1a. | Let triangle ABC be any triangle. | 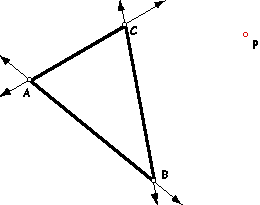 |
| Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. | 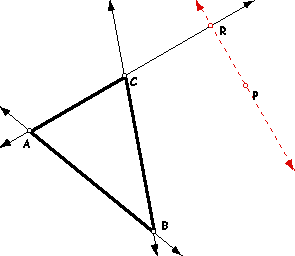 |
|
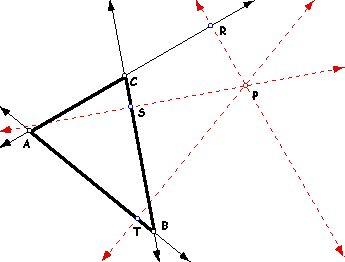 |
||
| Triangle RST is the Pedal Triangle for Pedal Point P. | 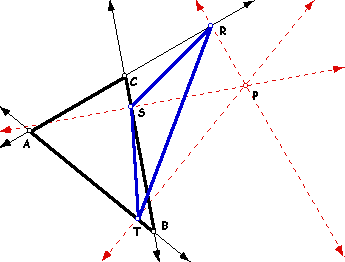 |
|
| 1b. |
Use GSP to create a script for the general construction of a pedal triangle to triangle ABC where P is any point in the plane of ABC. Click the image on the right to interact with the figure in Geometer's Sketchpad. Click here to download a GSP script to construct your own. |
 |
 |
Comments? Questions? e-mail me at blawler@coe.uga.edu |
| Last revised: January 2, 2001 |
|