Assignment 6

This exploration will look at question 9 of Assignment 6. Problem 9 looks at the set of points that is equidistant from a line, the directrix and a fixed point (assuming the point is not on the line). These points form a parabola.

Looking at the figure below, let P be the vertex and let P' be a point on the directrix. Point A is the measurement of A to the line since P'A is perpendicular to the line. A is also on the perpendicular bisector of PP', so that PA and P'A are congruent. The figure shows all of the points are equidistant from the directrix and the vertex.

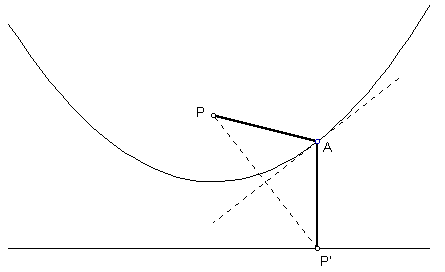
To look at the construction of this parabola using tangent lines in Geometer Sketch Pad click here.

Now we will exchange our line in the above example for a circle. Choosing a random point, P, inside of circle O and a point, P', on the perimeter of the circle we will now construct an ellipse. By definition an ellipse is a set of points that is the same sum from the distances of the vertices to that point. So we construct an isosceles triangle where P'A and PA are congruent. Since P'A + AO is a radius and the radius of the circle is unchanging then PA + AO must be equal to the length of the radius. So the sum of PA + AO is always the same which is the radius.

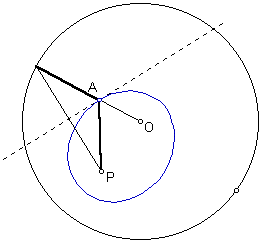
To look at the construction of an ellipse using tangent lines in Geometer Sketch Pad click here.

Here is a download to show how a hyperbola would be formed by moving point P outside the circle. Hyperbola formed by tangent lines.