Final Project

Jonathan Lawson

In this last exploration we will be looking at a given triangle and a given point, P, in the interior of the triangle.  Lines AP, BP, and CP will intersect the legs A, B, and C at points D, E, and F, respectively.

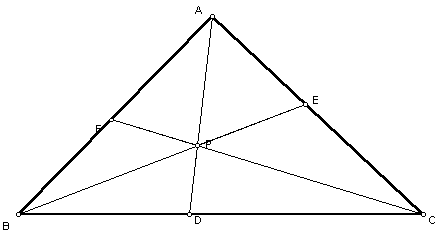
We want to look at the ratios in the above triangle.  If we move P anywhere in the triangle we have the ratio below:

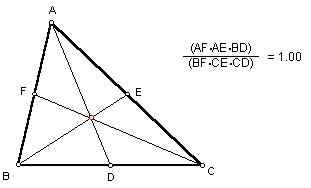
If you would like to manipulate this GSP file to see if the ratios change, click here.

So we first construct a line through point C parallel to AD, and extend segment BE to intersect the parallel line at point H.  We also construct a line through point B parallel to AD, and extend segment CF to intersect the parallel line at point G. 

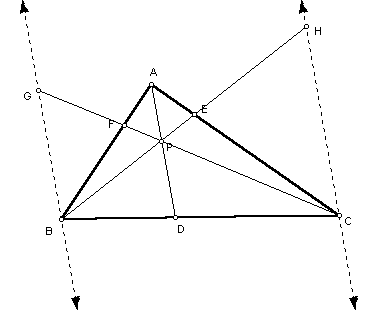
Angle BPD and angle BHC are congruent because they are corresponding angles and angle PBD is congruent to itself, so the triangles BPD and BHC are similar triangles.  Triangles CPD and CGB are similar by a similar argument just stated.  So we can get from the first set of similar triangles

and from the second set of similar triangles

and multiplying these equations together we get

This gets part of the equation we are looking for but I cannot determine the rest of the similar triangles that are needed to find the exact proportion. 

Finally we will look at the ratio of the areas of the triangles mentioned above when P is in the interior of the given triangle.

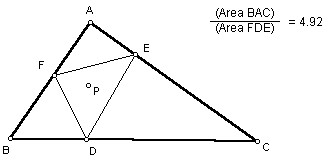
No matter where P is located within the interior of the triangle, the ratio of the areas is always greater than or equal to four.  Click here to download a GSP file which the triangle and point can be manipulated.  The one case where the ratio is equal to four is when point P is located at the centroid of the triangle.

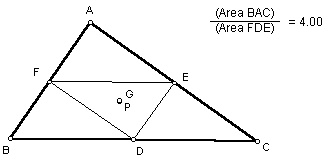
When the point P is located at the centroid of triangle ABC, the triangle is divided into four congruent triangles, and the triangle EFD is one fourth of the given triangle. 

Return