ASSIGNMENT ONE
Presented by Godfried Lawson

      In this assignment I will explore the graph of each of the following equations and prepare
a file of discussion.







 

Let examine the graph of




The graph of the above equation is a circle with the coordinate of center c(0,0) and one unit radius. The domain of the relation graphed above is all numbers between -1 and 1 included. The range of this relation is the same as the domain. A quick  vertical line test reveals that the relation is not a function. To interpret this relation, one can say that the sum of the square of the domain and the square of the range is 1.
 
 

Let examine the graph of : 

A close examination of the relation graphed above shows that the the relation is a function with the domain and the range equal to all real numbers.
Why this the range and the domain is all real numbers?


                                          X                       X^2                     X^3
                                         -2                                   4                               -8
                                         -1                                   1                               -1
                                    -0.75                            .5625                        -.4219
                                      -.50                                .25                          -.125
                                      -.25                            .0625                        -.0156
                                          0                                   0                                0
                                          1                                   1                                1
                                          2                                   4                                8

From the above table you can observe that a negative number raised to an odd exponent produce a negative result
and any number raised to an even exponent is always positive.
There are unlimited numbers of combination of  the sum of the cube of two numbers which equal to 1.
The equation x^3 +y^3 =1 can be expressed as y =  (1- x^3)^(1/3)
When x is a positive number greater than one, the expression in parentheses is negative.
When x is a negative  number less than one, the expression in parentheses is positive.
When x is equal to one,  the expression in parentheses is 0.
The equation x^2 +y^2 =1 can be expressed as y =  (1- x^2)^(1/2) and y = -(1 -x^2)^(1/2)
For any value of x greater than 1, the expression in parentheses is negative.  Therefore there is no real number value for y.
this is the reason why the domain and the range of such equation is all numbers between -1 and 1
 
 



Let examine the graph of: 





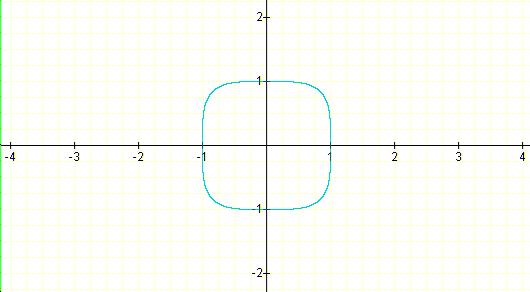
x^2 + y^2 = 1 is the parent function of x^4 + y^4 =1
Hence, the equation equation x^4 +y^4 =1 can be expressed as y =  (1- x^4)^(1/4) and y = -(1 -x^4)^(1/4)
When the value of x is less than 0.5 then, the expression in parentheses approaches 1

Let examine the graph of: 

This graph has all the characteristic of the graph of x^3 + y^3 = 1 , except that
the increase and the decrease in y goes in lower rate.

 Let examine the the graph of : 




When the value of x is less than 0.9 then, the expression in parentheses approaches 1

Let examine the graph of: 


.

             Click HERE to see the animation of:        and 
 
 


Return