

With the graphing calculator 2.7 I will investigate the graph
of:
* The investigation will focus on how different values of a,
b, and k affect the shape of the graph..
* I will compare the above equation with
* Then I will observe what happen when cos(k-theta
) is replaced with sin(k-theta
).
DEFINITION OF POLAR COORDINATE SYSTEM
The polar coordinate system is a system of coordinate in which
a point in the plane is identified by its distance r along a ray
from a fixed point (the pole) and by the angle theta
between a fixed line ( the polar axis ) and the ray
Every point P, other than the pole , can be represented by an
ordered pair of real numbers ( r, theta).
Before we observe the graph of :
Let observe the table and the graph of:
| Theta in degree | cos(theta) | 1 + cos(theta) | 1 + cos(2 theta) | 1 + 3cos(2 theta) |
| 0 | 1 | 2 | 3 | 4 |
| 30 | .15 | 1.15 | .05 | -1.9 |
| 60 | -.95 | .05 | 1.81 | 3.44 |
| 90 | -.45 | .55 | .40 | -.80 |
| 120 | .81 | 1.81 | 1.32 | 1.98 |
| 150 | .70 | 1.70 | .98 | .93 |
| 180 | -.60 | .40 | .72 | .150 |
| 210 | -.88 | .12 | 1.56 | 2.69 |
| 240 | .33 | 1.33 | .21 | -1.34 |
| 270 | .98 | 1.98 | 1.94 | 3.81 |
| 300 | -.02 | .98 | 0.00 | -2.00 |
| 330 | -.99 | .01 | 1.97 | 3.90 |
| 360 | -.28 | .72 | .166 | -1.51 |
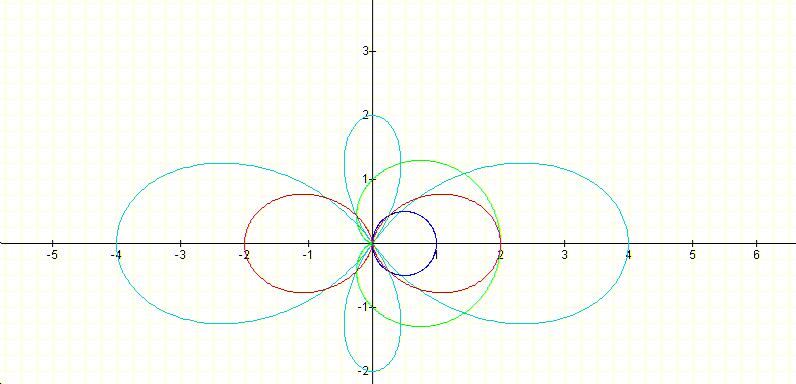
Polar graphs can be classified in families. The graphs of cos(theta)
( in light blue ) and sin( theta) ( not shown on the on graph
above ) are the the parents graphs of polar graphs.
Both graphs are circles with a diameter of 1 unit and both pass
through the origin. As with many families of graphs, you can alter
the position and shape of the graph by multiplying the function
by a number or by adding to it. You can also multiply theta by
a number or add a number to it to alter the graph.
Notice that the graph of the equation.
( in dark blue ) is symmetric with respect to the polar
axis, as is its parent graph .
However, the appearance of a small loop inside the outside graph,
which is no a circle, does not resemble the parent graph.
This graph is called a Limacon.
Polar equations of the form make graphs that
are called Rose. K is a positive integer.
Look at he graph of the equations below to see the pattern in
the amplitudes and in k-theta.
What happen when cosine is replace by sine?
( dark blue )
( green )
( light blue )
(red )
The difference between r = a + bcos (theta) and = a +
bsin (theta) is due to fact that
for any angle in standard position with measure theta , a point
p(x, y) on its terminal side , and ,
the trigonometric functions of theta are as follow;