

SECOND DEGREE EQUATIONS Presented by Godfried Lawson
In this assignment I will explore the graph of:
I will then replace each x by ( x - 4 ). I will comment on
my observations and on the behavior of the graph.
I will then change the equation to move the graph into the second
quadrant.
And finally, I will change the equation to produce a graph
that concave down and shares the same vertex.
Let examine the graph of:
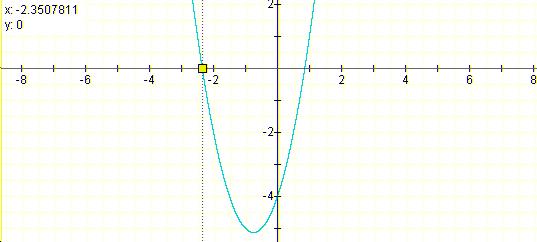
The graph of the equation is a parabola with the axis of symmetry equal to - 0.75 and the vertex of (-0.75,-5.125) The equation has two real roots. Since the leading coefficient is a positive number, the parabola opens up.
The graph lies in all four quadrants. The graph continuously increases its value in quadrant I and quadrant II.Let replace x in the equation above by ( x- 4 ) and overlay he new graph on the old one and see what can we observe.
The new equations:
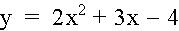
You can observe here that, the original graph has shifted four units to the right. This means that the x value on the original graph is increased by four while the y value remain the same.
Check the x value on the first graph when y = 0 ( the single graph above this one , then check the x value on the second graph when y = 0.( the green graph ).I will change the equation to move the graph into the second quadrant.
It is easy to maintain a line segment in a given quadrant. To maintain a graph that continuously increases, we must find a way to keep it look like a line. Therefore we must stretch the graph up and move it far away from the y-axis and just up of the x-axis. The leading coefficient can produce a rapid growth of the function and it can produce a rapid decay of the function. Since I want to keep my graph open up, the leading coefficient must remain positive and very large to produce a very rapid growth. This is one of such equations:and the graph is:
Click here to see how the graph shift on the x-axis and the y-axis as well as it stretches up with a variable leading coefficient
with the equation :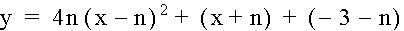
Let change the equation to produce a graph concave down that shares the same vertex.
the vertex of the the graph:
is: (-0.75,-5.125)
Therefore the vertex of the new graph must have the same coordinate. The equation of the axis of symmetry x = -b / 2a must remain the same. To produce a parabola that opens down, the leading coefficient a must be negative. The new equation must be in the form:Let find the value of c so that the vertex has the same x and y coordinate.
-5.125 = -2(-0.75)^2 -3(-0.75) + C
This implies C = -6.25. The equation is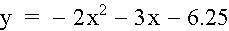
The graph of both equations is:
Let f1 is the given equation of the parabola and f2 the equation of the second parabola with missing c2 in such a way that:
f1= ax^2 + bx + c and
f2 = - ax^2 - bx , then
C2 = f1( -a/b) - f2(-a/b)