

In this assignment I will construct a triangle ABC and a point P. If P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC is called the Pedal Triangle. The three points R, S, and T of intersections are connected to form the pedal triangle RST with P, the Pedal Point.
I will conduct the following investigation about the Pedal point P:
**** What if pedal point P is the
centroid of triangle ABC?
*** What if . . . P is the incenter .
. . ?
*** What if . . . P is the Orthocenter
. . . ? Even if outside ABC?
*** What if . . . P is the Circumcenter
. . . ? Even if outside ABC?
You may notice that the slope of the line segment AC is the
same as the slope of the line segment RS.
Click HERE for a GSP sketch
to see the change in slopes and see this is not generally the
case.
The pedal triangle is always inside the original triangle ABC
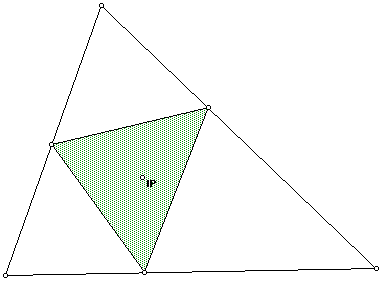
The pedal triangle is always inside the original triangle ABC. The vertices of the pedal triangle would be at the points of tangency of the incircle. That is, the incircle of ABC is the Circumcircle of the pedal triangle.
The pedal triangle is inside as well as outside the original
triangle ABC
The pedal triangle is always inside the original triangle ABC