instruct

Problem: Area of Golfing Greens
Mr. Lawson's 4 Th. period class.
North Clayton High School

Problem:

The greens keeper at a golf course needs to estimate of the areas in order to know how much fertilizer to apply to
the greens.
How to estimate the area of a golf green? Assuming that the green is flat.

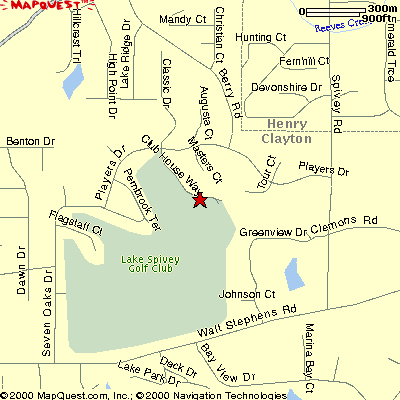
For our end-of-the-year project, we have to approximate the area of an actual golf course. Then we would find the price of fertilizer needed to cover this area.

Jaret Gant shrewdly searched for a local golf course map via the Internet. He went to Yahoo® and was able to secure a map of the Lake Spivey Golf Club.

Analysis:

In order to find the area of the golf course, we divided the golf course into ten geometric shapes:

Using the scale of the map, we estimate the dimension of each figure including the height (h). The dimensions are mesured in feet.

                      1--    Trapezoid: 1100' , 2700' , 1000' , 2700'
                2--    Trapezoid: 500' , 1200' , 700' , 500'
                3--    Trapezoid: 700' , 800' , 1000' , 800'
4--    Triangle: 300' , 600' , 800'
             5--    Trapezoid: 500' , 800' , 800' , 400'
              6--   Trapezoid: 500' , 550' , 400' , 150'
7--    Triangle: 500' , 200' , 600'
8--    Triangle: 400' , 500' , 800'
9--    Triangle: 200' , 400' , 500'
10--    Triangle: 200 , 400' , 500'

Calculations:

The formula for the area of the trapezoid is:
A= 1/2(a+b) h
The formula for the area of the triangle, using Hero's formula is:

A = sqrt(s(s-a)(s-b)(s-c)), where S= 1/2 (a+b+c)

a, b, c, are the sides of the triangle.

A = 1/2(1100 +1000) 2700 = 2,835,000
A = 1/2(500+1200) 500 = 425,000
A = 1/2 (800+1000) 800 = 720,000
S = 1/2 (1000+750+500) = 181,546
A= sqrt(1125 (1125-1000)(1125-750)(1125-500) =181,546
A = 1/2 (500+400)800 = 360,000
A = 1/2 (150+400) 500 = 137,500

                      S = 1/2 (500+200+600) = 650                A = sprt(650 (650-500)(650-200)(650-600) )
A = 46,837                       S = 1/2 (400+500+800) = 850                    A = sqrt(850(850-400)(850-500)(850-800))
A = 81,815                       S = 1/2 (200+400+500) = 550                    A = sqrt(550(550-200)(550-400)(550-500))
A = 37,997                       S = 1/2 (200+400+500) = 550                   A = sqrt(550(550-200)(550-400)(550-500))
A = 37,997

Total Area: 4,863,692 square feet

Let state the facts: Nia Mitchell and Kiamani Robey found that one 18 pound Vigoror Lawn Fertilizer bag covers 5,000 square feet and has a price of $5.93

The number of bags needed is 4,863,692 / 5000 = 973 bags; rounded to 1000 bags

The price of fertilizer needed to cover this area will be: 5.93( 1000 ) = $ 5930

Credits:

Godfried Lawson, Coordinator

Thang Ly, Taskmaster

Resource Specialists
Yolanda Fountain
Jaret Gant
Nia Mitchell
Kiamani Robey

Analysis
Brandon Dukes
Ngozi Ogbuehi

Data Interpretation
Tavy Vorn

Angela Aina, Scribe

Devin Cobb, Worker

Cartography
Trinh Nguyen

Calculations
Cuong Nguyen
Jeffery Anoka

Return