
By: Tim Lehman

Part A: Our final assignment starts with examining any triangle ABC and point P inside triangle ABC. We label the intersection of AB and CP as point F, intersection of BC and AP as point D, and intersection of AC and BP as point E. For a GSP sketch of this, click here.
Part B: Now, we measure AF, BD, CE, FB, DC, and EA. On the sketch, we can see (AF)(BD)(CE)=(FB)(DC)(EA).
First, let's examine triangle ABC further.
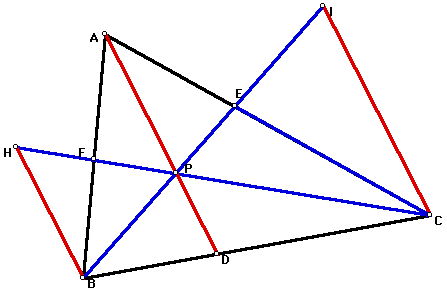
Again, triangle ABC and point P are given and E,D, and F are defined as before. Define IC and HB as parallel to AD. Because alternate interior angles of parallel lines are equal and vertical angles are equal, we have angle-angle similarity of triangles (FHB) and (FPA) and of triangles (ICE) and (PAE). We can draw parallel lines to the other two lines from a vertex through P and get more similar triangles. Click here for a GSP sketch where all the triangles of the same color are similar. We know corresponding sides of similar triangle are proportional. I feel somewhere herein lies the proof. However, I have been unable to arrive at it. With pages of sides that are equal, I cannot end with the equation desired. I thought by using the fact (in the diagram above) that both similar triangles sharing AP would in some way complete the proof. (Or, after drawing all six pairs of similar triangles, the shared sides would bring me closer to the answer.)
After cheating and looking in a book (Modern Geometries by J. Smart), I see the proof uses Ceva's theorem after applying Menelaus' theorem.
We start with triangle ABC. Menelaus' theorem shows that
(AP)(DC)(BF) is equal to 1. Similarly, (AE)(CB)(DP) is equal to 1. . ., (PD)(CB)(FA) ....................................... (EC)(BD)(PA)
By multiplying these two, we see that (AE)(CD)(BF)=(EC)(BD)(FA), as desired.
It remains to see Menelaus' theorem. It states that if three points which are on each side of a triangle are colinear than the ratios of division of their sides is 1. From the diagram below, note that (ADG)~CFG, BEI~CFI, and BEH~ADH.
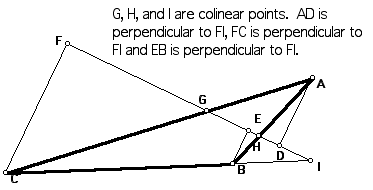
This would imply that (AG)/(GC)=(AD)/(CF), (CI)/(IB)=(CF)/(BE), and (BH)/(HA)=(BE)/(AD). Thus, [(AG)(CI)(BH)]/[(GC)(IB)(HA)] =[(AD)(CF)(BE)]/[(CF)(BE)(AD)]=1
The problem can be expanded by examining point P outside the triangle ABC with D, E, and F defined as before (only looking at intersection of lines instead of line segments.) For a GSP sketch, click here.
Note that our equality from before still holds when point P is outside triangle ABC.
Part C: Lastly, we want to examine the triangle DEF.
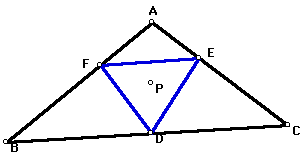
The claim is the area (DEF) is at most 1/4(area (ABC)). For the adventurous type, here is a GSP sketch with which this can be investigated.
First, let's see the area of (DEF) can equal 1/4(area (ABC)). When P is the centroid, this would occur. If P was the centroid, D, E, and F would be the midpoints of sides BC, AB, and AC, respectively. By side-angle-side similarity,(AEF) is similar to ABC. Thus, angle AEC=angle ABC so EF is parallel to BC. Similarly, DE is parallel to AC and FD is parallel to AB. Using the angles that must be equal and the fact that D, E, and F are on the midpoints, we can see that all four triangles are conguent. Thus, area (triangle (DEF))=1/4(area (triangle (ABC))).
Now, we want to see the area of (DEF) must be no more than 1/4 (area (ABC)).