
by Becky Dragan and Tim Lehman

First, we want to examine triangle ABC. We first note that orthocenter of the triangle ACH (with point H the orthocenter of triangle ABC) is point B. Because H is the orthocenter of triangle ABC, we know line HC is perpendicular to line AB. Thus, the altitude from point A to side HC lies along line AB. Similarly, the altitude from point C to side AH is along line BC. Therefore, the orthocenter of triangle ACH is at the intersection of lines AB and BC, which is point B. We can use similar arguments to note points A and C are the orthocenters of triangles CBH and ABH, respectively. If you are having trouble visualizing this, check out a GSP sketch.
Now, let us shift our focus to the circumcircles of triangles ABH, ACH, and BCH. When we examine a GSP sketch with circumcenters O, I, and L, it appears the circumcircles are all equal and that the triangle formed by the circumcenters is congruent to the triangle ABC.
First, we will examine the three circumcircles. We want to see all three have the same radius. By construction, we only need to show one of the three circumcircles is congruent to circle ABC. We will prove this using 2 cases.
Case I: Assume H is on the greater arc AC.
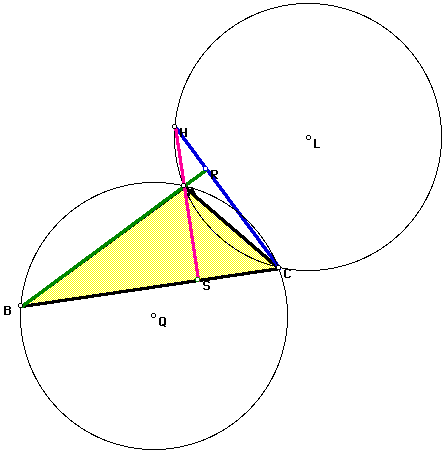
Assume angle CHA = x. Because H is the orthocenter, line BA is orthogonal to HC at some point R and HS is orthogonal to BC at some point S. So, angle BRC and angle HSC are both equal to 90 degrees. Triangle HSC and triangle BRC share angle RCS. Thus, since the sum of the interior angles of a triangle is 180 degrees, angle RBC is equal to angle CHS. It immediately follows that angle CHA is equal to angle RBC (angle ABC). Since angle CHA = x, angle ABC = x. Angle ABC is an inscribed angle in circle ABC and it intersects the arc AC. It is thus equal to twice the central angle that intersects the arc AC. This central angle is AQC. Since angle ABC = 2x, angle AQC = 2x. By the same argument for angles AHC and ALC of circle AHC, angle ALC = 2x. So angles AQC and ALC are equal. By definition of a circle, triangles AQC and ALC are isosceles triangles.
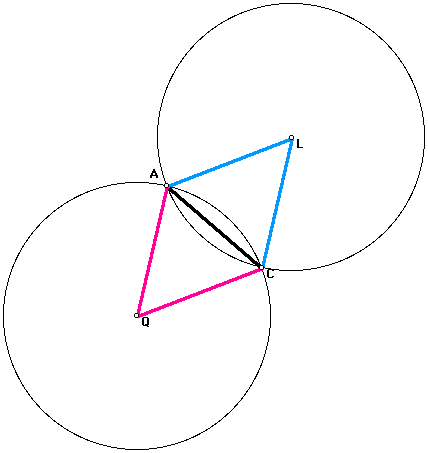
Since triangle AQC is an isosceles triangle, the base angles -- angle CAQ and angle ACQ are equal. We will call each of these angles w. Since triangle ALC is an isosceles triangle, the base angles -- angle CAL and angle ACL are equal. We will call each of these angles z. By the triangle angle sum theorem, the sum of the interior angles for triangle AQC are equal to the sum of the interior angles of ALC, so
2x + w + w = 2x + z + z
2w = 2z
w=z
So the base angles of the two triangles are equal. The two triangles share side AC. So by angle-side-angle congruence, triangle AQC is congruent to triangle ALC. So AQ is equal to AL. Thus, the two circles have equal radii and are congruent.
Case II: Assume H is in the minor arc AC.
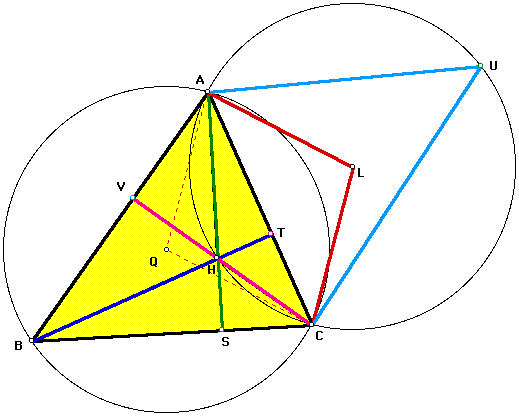
Let the central angle, angle ALC, be equal to 2x. Because the inscribed angle AUC cuts chord AC (as does the central angle ALC), angle AUC is equal to 1/2 the measure of angle ALC. So angle AUC=x. Opposite angles of inscribed quadrilaterals are supplementary, so angle AHC=180-x (AUCH is an inscribed quadrilateral). Angles AHC and VHS are vertical angles, so angle VHS=180-x. Since angles HVB and HSB are right angles, the sum of angles VHS and VBS must equal 180 (for quadrilateral VHSB). So angle VHS + VBS = 180,
180-x+VBS =180
VBS = x. Thus angle ABC = x. The inscribed angle ABC cuts the chord AC as does the central angle AQC. So, the central angle AQC = 2x. Hence angle AQC is equal to angle ALC. From case I, we saw that two isosceles triangles that share the same base and have an equal angle are congruent. So triangles AQC and ALC are congruent. So AQ=AL and the two circles are congruent since they have radii of equal measure.
Special thanks to Keith Leatham for his assistance on part of this proof.