---

By Tim Lehman

---

Assignment 9: Pedal Triangles

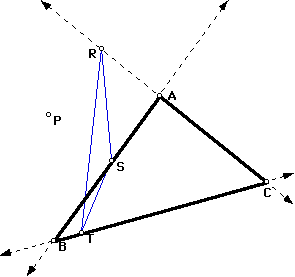
The pedal triangle is formed from a given triangle ABC and a point P. Pedal triangle RST is formed by the intersections of the lines perpendicular to lines AB, BC, and AC. An example is shown below.

Click here for a GSP script to make the pedal triangle of a triangle ABC with pedal point P.

Further study can be done by moving point P. Some interesting cases include when P is the incenter, centroid, orthocenter, and circumcenter (clicking on each type of center provides a GSP sketch example).

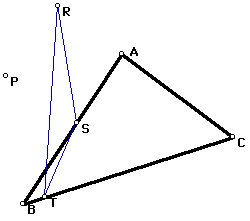
Another way to set P is to require it to be on the boundary of triangle ABC, as it is here in a GSP sketch. Note that the pedal triangle has a vertex at point P and that when P is at a vertex of triangle ABC that the pedal triangle degenerates.

So far, we have examined the pedal triangle when given the pedal point and given triangle. Another way to study pedal triangles is to look at the possible triangles from a given pedal triangle and pedal point. Click here to see a sketch of this or here for a GSP script.

To determine the given triangle, we consider the reverse of our method of finding the pedal triangle. Given pedal triangle RST and pedal point P, first construct the three lines connecting P to R, S, and T.

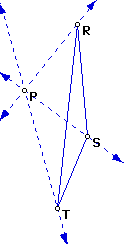
Next, we construct the line perpendicular to PT and passing through T, the line perpendicular to PS and passing through S, and the line perpendicular to PR and passing through R.

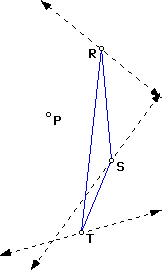
By finding the intersection of these lines, we have our original triangle ABC.