
Lesson 4: Introduction of area
By: Tim Lehman

Previous lessons in the unit have included definitions of different types of polygons (rectangles, squares, parallelograms, triangles, etc.) and circles and perimeter and circumference. It is assumed the students have some experience with area (part of elementary curriculum). This lesson will explore area primarily using GSP. If GSP is not available, geoboards could be substituted.
The class can start by drawing a segment connecting two points as below on GSP with grid shown and "Snap to Grid" on.
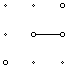
This segment will be considered to have a length of 1 unit. For the rest of the class, measurements will refer to this as a unit. Because the grid on GSP can be altered, it is difficult to attempt to use other units (such as inches, centimeters, etc.) One way to get around this is to have the class set their grids so this length is 1 in. or cm. Though not exact, this approach would give the students the opportunity to check their work later on by having GSP measure the area of the figures to see if it is similar to their answers.
Next, the class can construct a 1x1 square.
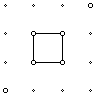
What is the area of a 1x1 square? Students will recognize the area of this square is 1 unit squared. Though they understand how to find area, some do not have a grasp of what area is. Thus, a possible follow-up question would be: How would you define area?
The class can then move on to the area of rectangles.
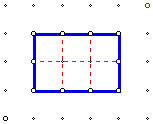
The goal is to generalize that the area is length x width. In
the diagram above, the area can be seen as 3 groups of 2 1 x 1
blocks so it has an area of 3*2 = 6 units squared .
EXERCISE: Are area and perimeter related? The class can look at different rectangles and see if ones with larger areas always (or ever) have larger perimeters. Click here for a GSP sketch with animation that might help.
Next, the class can find the area of different
right triangles. The goal is the class will see right triangles
are half of a rectangle so their area is ![]() lw.
lw.
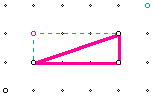
EXERCISE: Can two different polygons have the same area? The class should realize shapes that look different could cover the same area.
Tangrams would be a great way to get this idea across (and introduce problem solving.) Click here for a link to some interesting work Kent Wiginton has done with tangrams.
After right triangles and rectangles, the next
figure looked at should be parallelograms. After examining different
parallelograms,
we want to see a parallelogram is made up of two equal right triangles
and a rectangle. To generalize, the area is the base times the
height.
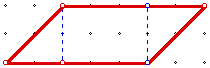
(NOTE: It is not easy to see this with all parallelograms on the geoboard-usually when there is not one side parallel or perpendicular to the bottom of the geoboard. GSP does not have this limitation.)
The area of triangles (non-right) remains. As the right triangle is half of the rectangle, a triangle is half of a parallelogram. (A rectangle is a parallelogram with right angles. A right triangle is a triangle with a right angle. Thus, this makes sense.)
EXERCISE: Find different triangles with the
same base and the same area
In the example below, the dotted triangles have the same area
because they have the same height and base as the original triangle.
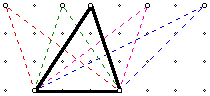
Click here for a GSP sketch of the above example.
The class can now work with "odd" polygons, like the one picture below. After estimating the area, the class can determine how to measure the area. GSP can be used to construct segments that divide the shape into parts that can be found.
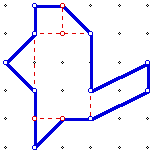
Finally, the class can find area of their own unique shapes and then challenge their classmates to figure them out.