
How do you find the triangle with 1/3 of the area of the original triangle?
By: Tim Lehman

The triangle we will construct will not only be 1/3 of the area of the original triangle but also similar to the original triangle. For the new triangle to make both of these true, the sides need to be in a 1 to square root of 3 ratio with the sides of the original triangle. If the sides are of this ratio with the original, then the height of the triangles are as well (remembering the two are similar.)
The questions remains:
How can we find the length of the side with this ratio?
The side length can be found be constructing a 30-60-90 triangle with the length of the leg opposite of the 60 degree angle the same as one leg of the original triangle.
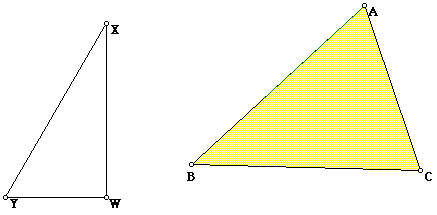
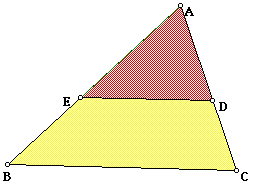
In the above sketch, triangle ABC is the original triangle. XW is equal to AC and angle XYW= 60 degrees, angle XWY=90 degrees, and angle YXW is 30 degrees.Thus, the ratio between YW and AC is square root of 3 to 1. By constructing point D such that AD=YW and constructing segment ED such that ED is parallel to BC, we now have a triangle ADE that is similar to ABC and is 1/3 of its area.
Any suggestions on ways to
word this page better would be appreciated.
Return