

Exporation 1: Dividing a triangle into 3
triangles of equal area
Method
I: After trisecting one side of a triangle (side BC below),
connect the opposite vertex (point A) to the two points that trisect
the side (H and I). Because the side is divided into three equal
segments, all three triangles have the same length of base and
height. Thus, all three triangles are of equal area. Click
here for an interactive GSP sketch of the example below.
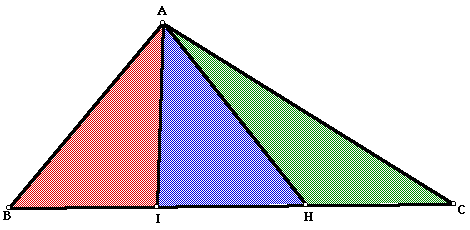
Having trouble trisecting a side of a triangle? Click here.
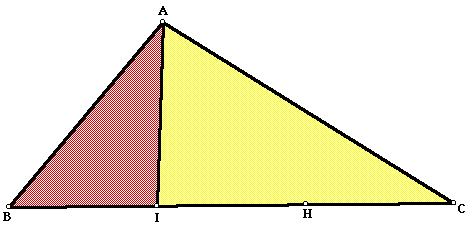
Method II: In many ways, method II is simply a variation of method I. After trisecting one side of a triangle, construct a segment connecting the opposite vertex (point A) to only one of the points trisecting the side (I). We then have two triangles. One (ABI) is equal to 1/3 the area of the original triangle (ABC). The other triangle (AIC) is 2/3 the area of the original triangle (ABC).Click here for a GSP sketch of the below.
To trisect the original triangle, we need to divide the larger triangle (AIC) into two equal triangles. This can be accomplished by finding the midpoint of any side of the triangle and constucting the segment from them to the opposite vertex. The two possibilities can be seen below.
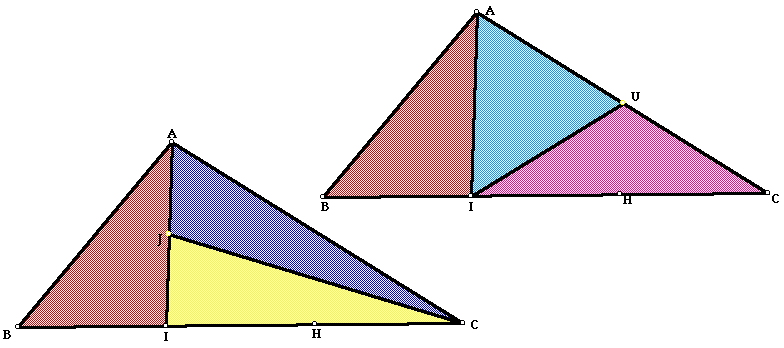
Method III:
Another way to divide a triangle into three triangles of equal area is to find the centroid (the point where the medians intersect). After determining the centroid (point G below), construct the segments connecting the vertices to the centroid. The three triangle created are of equal area.
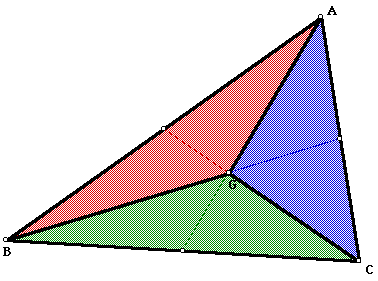
Click here for a GSP sketch of the above triangle.
What are some other ways to divide the
triangle into three equal triangles?
Exploration
2: Dividing a triangle into three equal pieces
The
first exploration only considered cutting the original triangle
into three equal triangles. Now we will examine two methods of
dividing the triangle into three equal parts that are not all
triangles.
Method I:
This method follows directly from method III above. The sides of the three equal sections are formed by connecting the midpoints of the three sides of the original triangle to the centroid. The reasoning of why it works is the same as in method III.

Click here for a GSP sketch of the above diagram.
Method II:
Another method of dividing the triangle into three equal portions includes dividing it into one triangle and two trapezoids. First, we will find the triangle that has an area of 1/3 the original triangle and has a side parallel to a side of the given triangle. How? Then, we divide the remaining area in half with a segment parallel to the side of the smaller triangle. Where would this segment be? We now have two trapezoids and a triangle that are each 1/3 of the area of the original triangle.

Click here for a GSP sketch of a triangle trisected using this method. (This sketch contains all construction lines as well.)
A variation of this method would be to divide the bottom two thirds in two other trapezoids. Let Q be the midpoint of LM and R be the midpoint of BC. The two trapezoids would have the same height and both bases would be the same length. Thus, the two would have the same area.

What are other ways to divide a triangle into three equal pieces?