
>
<

The quadratures of lunes, which were considered to belong to an uncommon class of propositions on account of the close relation of lunes to the circle, were first investigated by Hippocrates. His exposition was thought to be correct; we will therefore deal with them at length and describe them. He started with, and laid down as the first of the theorems useful for the purpose, the proposition that similar segments of circles have the same ratio to one another as the squares on their bases. And this he proved by first showing that the squares on the diameters have the same ratio as the circles.
Before continuing we should note that Hippocrates is trying to 'square a lune' by which he means to construct a square equal in area to the lune. This is precisely what the problem of 'squaring the circle' means, namely to construct a square whose area is equal to the area of the circle.
After proving this, he proceeded to show in what way it was possible to square a lune the outer circumference of which is that of a semicircle. This he affected by circumscribing a semicircle about an isoceles right-angled triangle and a segment of a circle similar to those cut off by the sides. Then, since the segment about the base is equal to the sum of those about the sides, it follows that, when the part of the triangle above the segment about the base is added to both alike, the lune will be equal to the triangle. Therefore the lune, having been proved equal to the triangle, can be squared.
In general his argument was based upon three preliminary result
Before we proceed more let us ask ourselves, what is a Lune? A lune is a figure in a plane that is bounded by two circular arcs as shown below. Basing our argument

on Hippocrates' second point, we can investigate it by demonstrating that an angle inscribed in a semicircle is right by using gsp. Construct several semicircles of different sizes as shown below.

We can therefore conclude that a triangle in a semicircle is a right triangle.For more demonstration, click here and here for the proof.
As it can be noted from his third point that the areas of two circles or semicircles are to each other as the squares on their diameters. What now can we conclude about the relationship between the areas of two semicircles and their diameter?
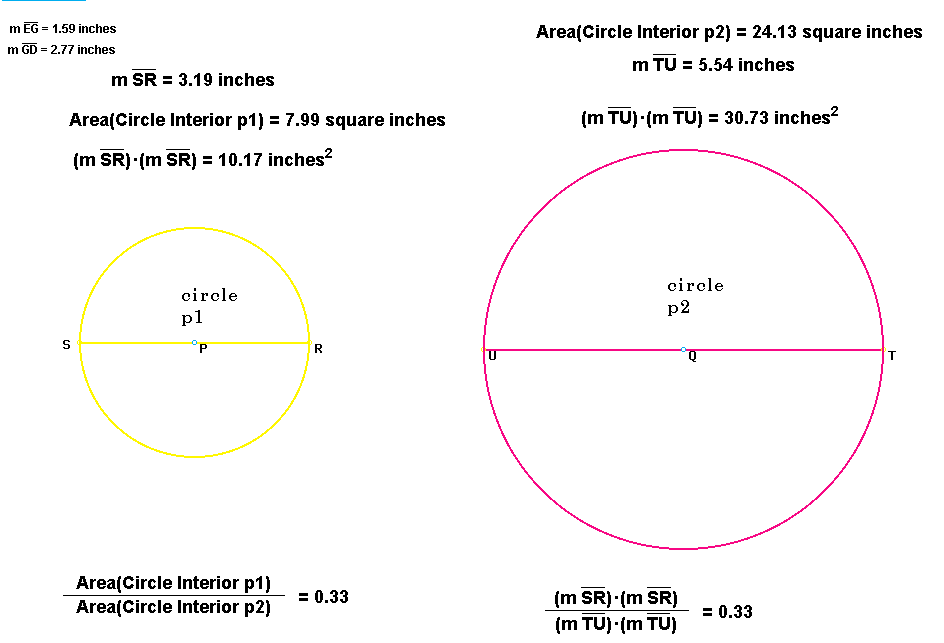
For more demonstration, click here to see animation. Now as shown above, the ratio of areas of the circles equals the ratio of the squares of the diameters then.

With all this investigation, what is the area of the lune? To investigate this let us construct the diagram as shown below.

In the diagram above (or click here).
(a) What relationship do you think is between triangle COA and COB? It can be noted that they are congruent because CO = OA = OB = radius.
(b) Now what do you think about CA and CB? are they equal?
To investigate this, the theorem of Pythagoras can of great help.

(c) As noted above about the two semicircles and their diameters, then:


Therefore the area of the semicircle CEA = 1/2 the area of the semicircle ACB
(d) Note that the area of the quadrant (CFAO) = 1/2 the area of the semicircle ACB
therefore the area of the semicircle CEA = the area of the quadrant CFAO.


AEC + ADC
equals semicircle ACE = quadrant CFAO which equals


ACE + triangle ACO
Therefore we can subtract area of section CAE and we are left with Area (Lune ACE) = Area (Triangle AOC) as shown below or
click here for the file that created the image. Finally with the area of lune equal to the area of triangle, then the lune can be squired as follows.
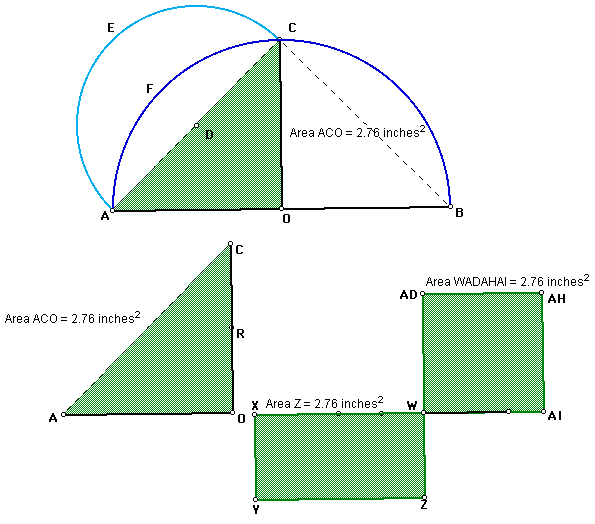
With all what hippocrates had done, it is still not possible to square a circle, click http://jwilson.coe.uga.edu/EMT668/EMAT6680.2001/Hays/GeometryProject/
to inverstigate more of such construction.
References:
Dunham, William. Journey Through Genius: The great Theorems of Mathematics.
Benjamin, Bold. Famous Problems of Geometry and How to solve them.
Heath, Thomas. A History of Greek Mathematics, Vol.1. Oxford, London, 1921. pp. 168&endash;169.
Burton, David M. Burton's History of Mathematics
http://www.maths.uwa.edu.au/~schultz/3M3/L3Hippocrates.html
http://users.ncia.net/~bobmead/hippoc2.htm
http://www.mathpages.com/home/kmath171.htm
http://www-groups.dcs.st-andrews.ac.uk/~history/HistTopics/Squaring_the_circle.html
http://www.geocities.com/vidkid_allison/leonardo/leo_lunkey.html
http://www.988.com/Biographer/Chios.htm
http://www.geometry.net/Scientists/Hippocrates_of_Chios.htm
http://www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/Hippocrates.html
http://www.geometry.net/scientists/hippocrates_of_chios.php
Back project page