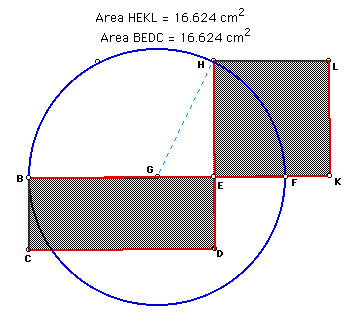
Let us construct rectangle BCDE. Using the rectangle, construct a square having area equal to that of BCDE. Extend line BE to the right and mark of EF with length equal to that of ED. Note that ED is equal to EF as shown below. Construct segment BF and find its midpoint. Using the midpoint as the center, construct the circle as shown below. Extend line DE to H and construct the point of intersection of the line and the circle. Using line EH construct the square EHLK as shown below. From the gsp image below, it can be noted that the area of the rectangle and square remains the same as we vary the area of the rectangle click here to see the animation And click here for the proof.

Back project page