In this assignment we will explore pedal triangles. Let us first construct a pedal triangle, let triangle ABC be any triangle and any point p in the plane as shown below.

Then we will construct the perpendiculars from point p to each of the sides of the triangle. It should be noted that depending on the triangle we may need to extend the sides so that the perpendiculars will intersect the lines as shown below.

Then finally, construct the points of intersection of perpendicular lines and the sides of triangle ABC. Use points SRT as points of intersection as shown above. Then connect this points (SRT) the triangle obtained, is the pedal triangle which is colored red blow.

If you happen to be interested in more exploration with working examples in GSP, click here. For general construction of a pedal triangle RST of triangle ABC click here for script.

What happens when if pedal point p is the centroid of triangle ABC? If p is in the centroid, then the pedal triangle becomes orthic triangle. Note that the orthic triangle is made by connecting the feet of the perpendiculars as shown below.

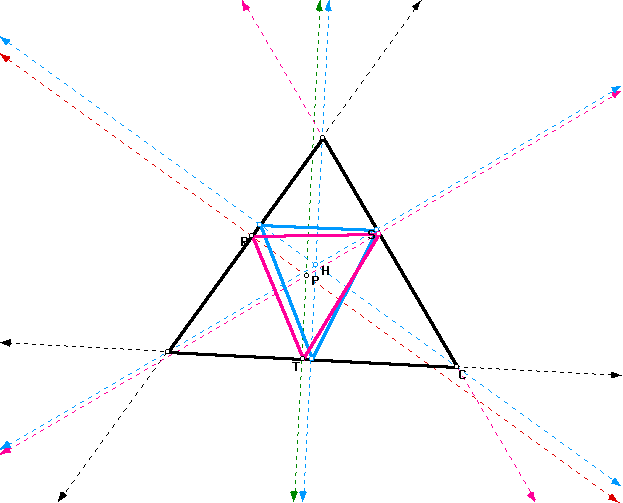
Try to construct perpendicular lines from H towards triangle ABC as shown below. It can be noted that the lines passes through EFG which happen to be the orthic triangle.

Now if you consider H as our P, then the pedal triangle would be like the one seen. Now try to play here with GSP , try to move P towards H and take note what happens. As P tend toward H It appear as if the red one will coincide with the blue which is the orthic triangle. The triangles and perpendiculars begins to line as illustrated below.