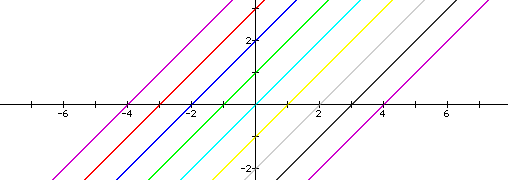
To begin this exploration, let us have a general Equation y=x+n , where n = -4 to +4 (i.e let the first equation passing through -4 be y=x-4 and the one passing through -3 be y=x-3 etc). It can be noted that as the value of n changes the shape of the graph does not change but it is simply changes position. Note that the Slope of the line and it's Shape does not change but only the position changes. Due to change of position, both the y and the x intercepts are affected as noted in the diagram and the Graphing Calc #0.
Next Graph
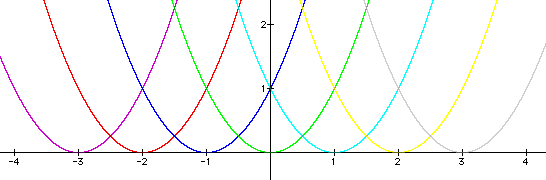
The Graphs above represent a general Equation
, where n =-3, +3. The Graph passing through (-3,0)
is 
. As it can be noted from a bove, the
shape and the general Slope of the Graphs do not change as the
value of n changes. Note that as n changes, the position of the
Graph is pushed along the X - axis therefore affecting only the
position and the respective X co-ordinates of each Graph. It can
be noted that as the parabola moves, it is tangent to the x -
axis hence each having one real root. Click Graphing
Calc # 00 for more illustration.
Back to Samuel's page
03 -18 - 2001