The objective of this writeup is to explore results from varying coefficients and power of certain parametric equations. I will investigate what will happen to by :

1. Varying values of a and b in the equations

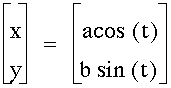
11. Varying values of a and b in the equations

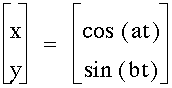
1. varying values of a and b in the equation

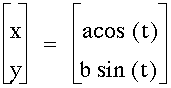
Let us try to vary the coefficients a and b in the trigonometric equation. If we let a = b and t ranges from 0 to 2p

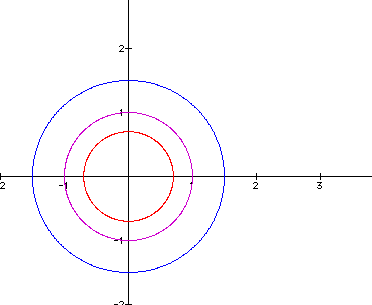
The graph above a=b =1; a=b =1.5; a=b =0.7 for t from 0 to 2p

One should note that the graphs are circles centered at the origin with radius a. This is so because:

x^2 + y^2= a^2(cos(t))^2 +a^2(sin(t))^2 =a^2[(cos(t))^2 +(sin(t))^2] =a^2 +y^2 =a^2 is the equation of circle of radius a and centered at the origin.

Now suppose a > b, and t runs from 0 to 2p suppose we let 1. a = 1.5 and b = 1, 11. a =2 and b =1.5, 111.a =2.5 and b = 2

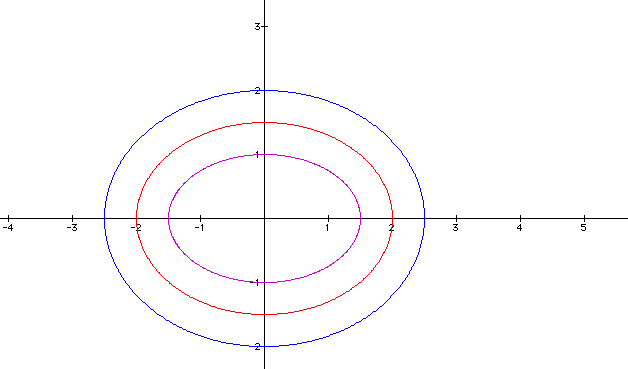
the graph will be an ellipse centered at the origin as shown above. Let us investigate why? notice x^2 = a^2 (cos(t))^2 and y^2 = b^2(sin(t))^2, therefore x^2/a^2 + y^2/b^2 = cos(t)^2 + sin(t)^2 = 1 Ok! Therefore for a > b in this case is an equation of ellipse with the major axis along the x - axis and center (o, o)

What do you think will happen when a<b

try 1. a = 1 and b = 1.5 11. a = 1.5 and b = 2 111. a = 2 and b = 2.5

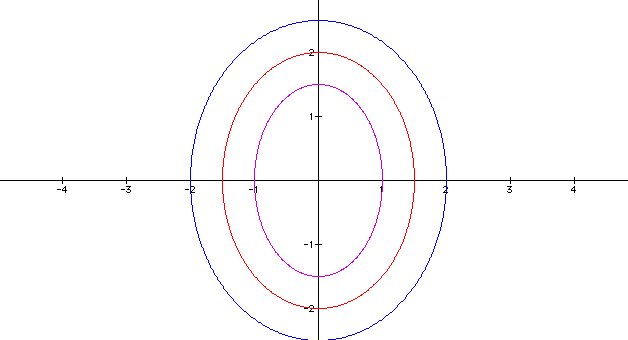
Case 11. Varying value of a and b in the equation of

x = cos(at)

y = sin(bt)

Notice the position of a and b in this case. Let us vary a from 0.5 to 1.5 to 2 but keep b constant at b =1 while t ranges from 0 to 2p

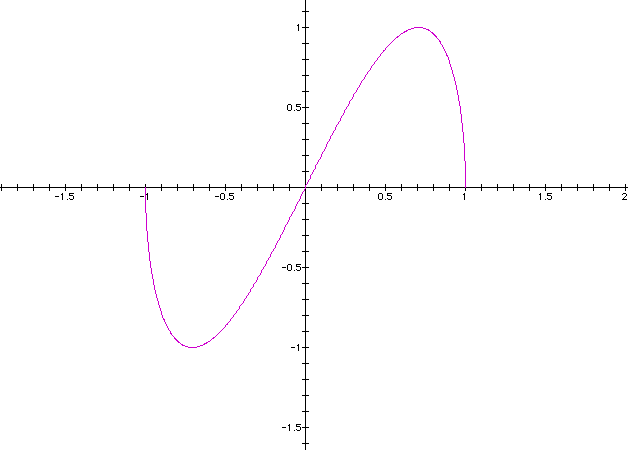
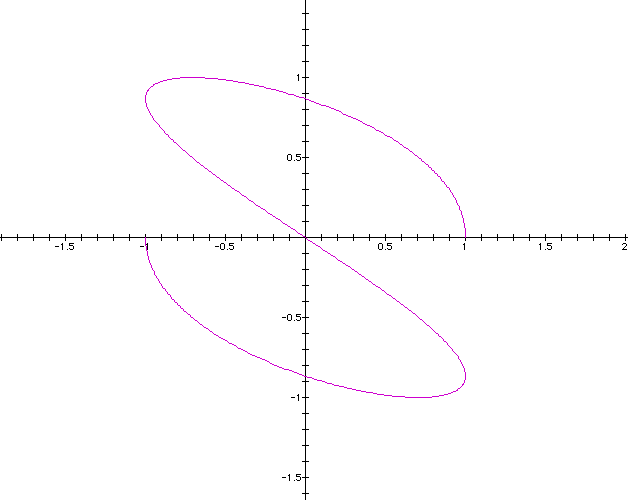
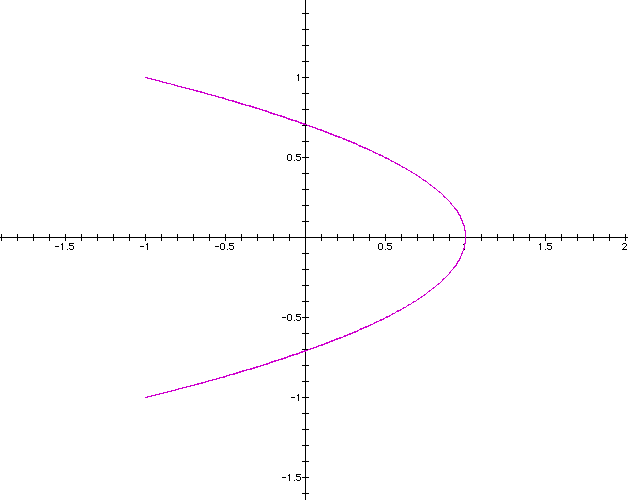
Now suppose we let t ranges from 0 to 2p the following graphs will be obtained.

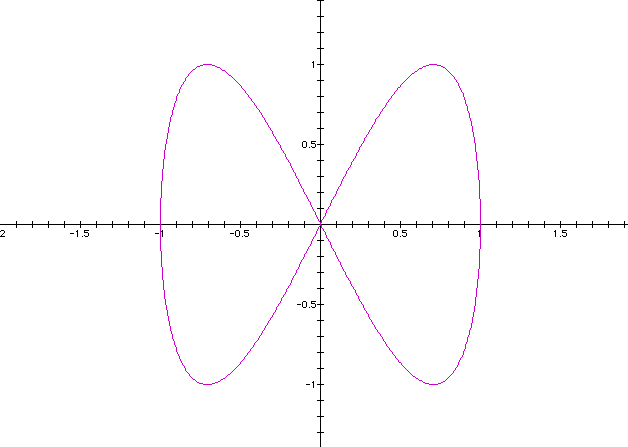
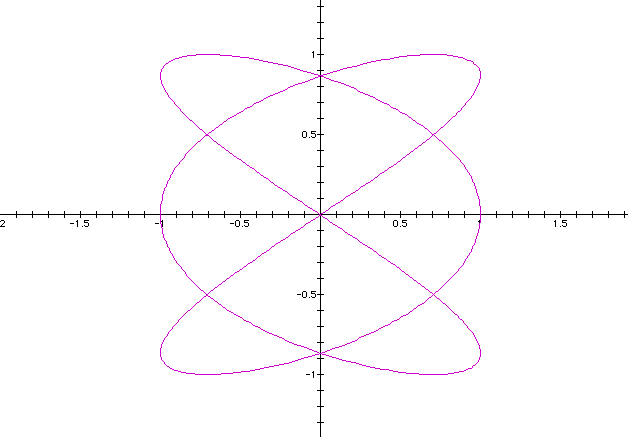
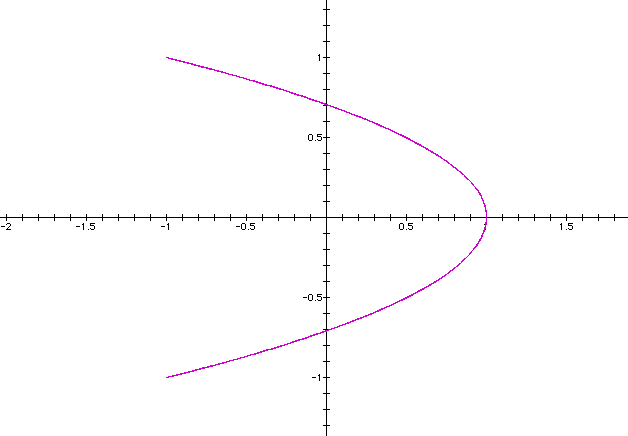
Notice that the curves do close for a =0.5 and a = 1.5, but for a = 2 ; the graph appear to be oscillating along the curve for a = 2

for more exploration here for graphing calculator animation

Let us vary b i.e b = 0.5, 1.5 and 2 , but let a = 1

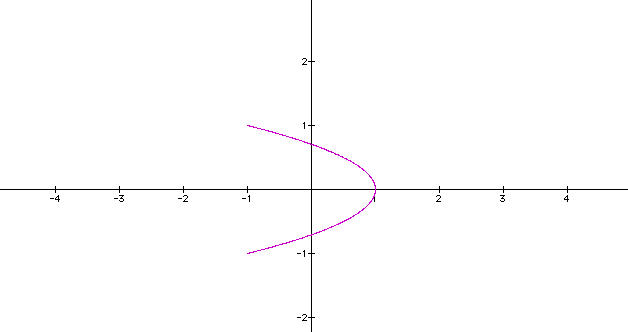
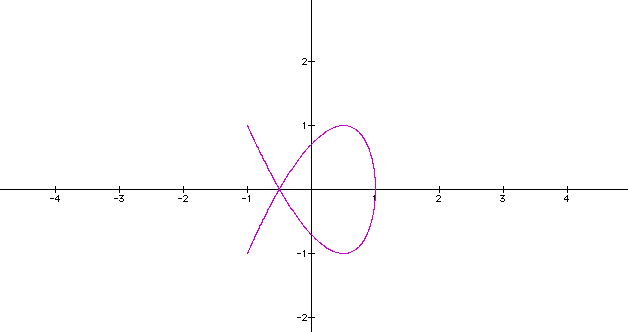
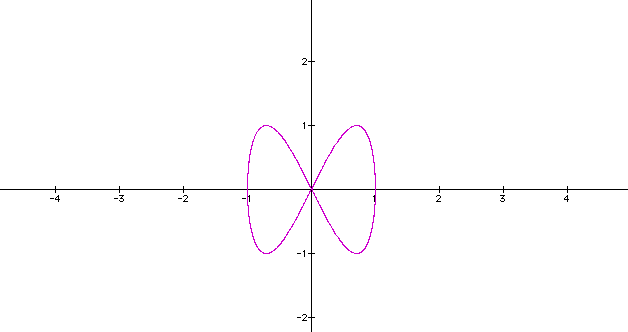
One can note that the two graphs (i.e one keeping a constant and keeping b constant) do not match . Click here fore graphing calculator for animation to see what I'm discussing.

Back to Samuel's page