In this investigation we will investigate polar equation of the form r = a + bcos(kq), where a, b and k are real numbers. To start with let us consider the following equations.

r = cos(q)

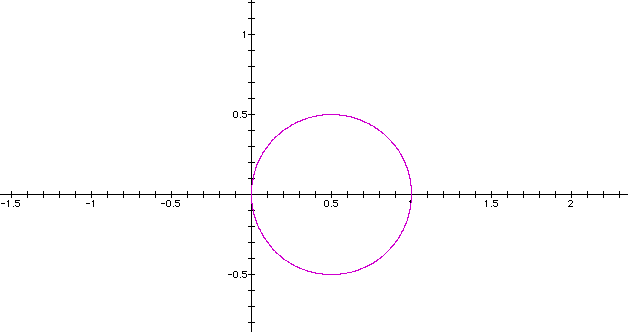
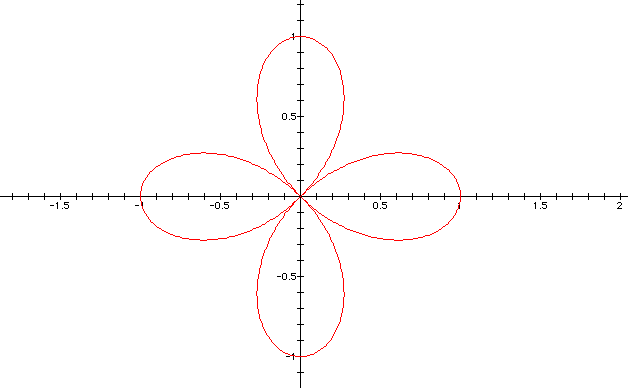
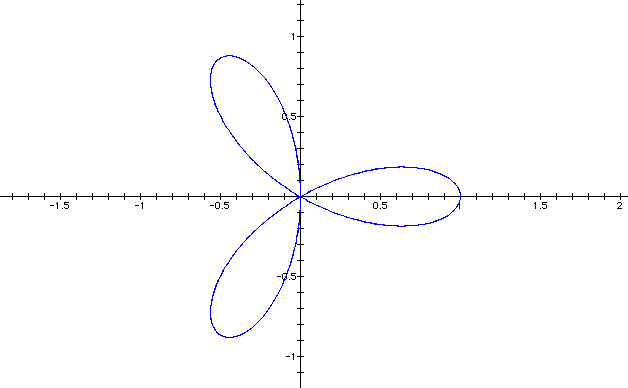
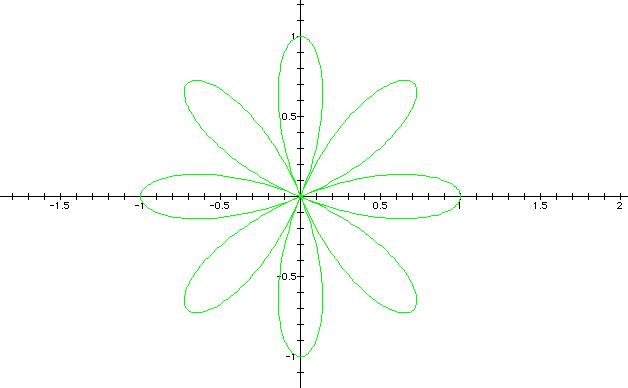
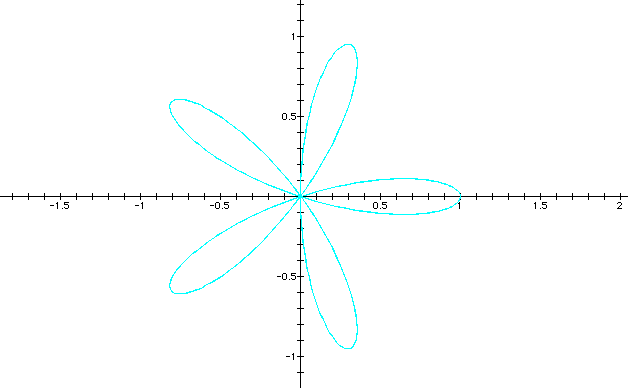
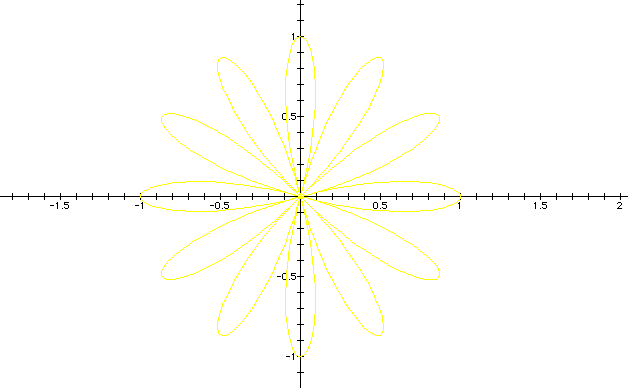
From the above observation one can note that when k is even, the graph always has 2k petals; whereas when k is odd the graph contains only k petals. For more information click here to download the graphing calculator file that was used to create the images. use different values of n in this case.

Let us consider if we multiply the functions by a given constant. See below for example

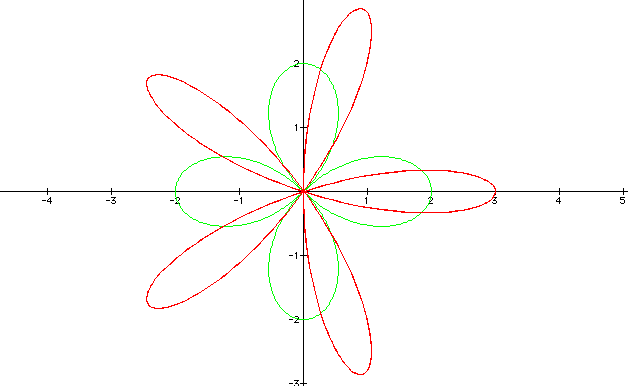
The reader should note that each equation color matches with the one of the graph. It can be noted that each petal is stretched (or shrink) to that value of the constant that multiply the equation. For more exploration click here to download the file that created the above image.

Suppose we add a constant to a to each of the equation above. see below for examples.

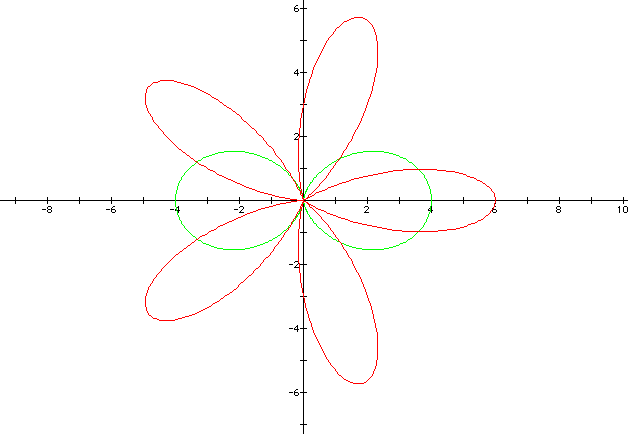
The observation made here is that the when k is multiplied by an even number k, no longer produces 2k petals as observed earlier. Note that adding a constant to the functions stretches the petals by the amount equal to this value. Notice that we have used the same value for a and b, let us see what will happen if different value of a and b are used. See the following examples

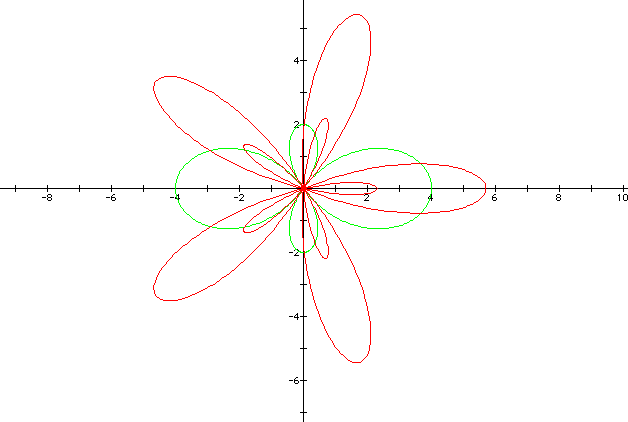
This now looks like a flower with petals of different length. For more investigation by using different values of a and b, click here to download the file that created the above image. One should note that there is a lot to be investigated with equations of this nature.

Back to Samuel's page