Introduction

In this write-up, I investigates the construction of the nine-point circle and prove that it exists. First, I look individually at the definitions and circumcircles of the medial triangle, orthic triangle, and orthocenter mid-segment triangle. Then, I put the three triangle together and hypothesize that their circumcircles coincide when the three triangles are constructed in the same given triangle. Finally, I call this common circumcircle the nine point circle of the original triangle, and I proof that the hypothesis is true.

Medial Triangle

The medial triangle of a given triangle is constructed by connecting the midpoints of the three sides of the given triangle. Take a look at the following example:

It should be noted that G is the centroid (intersection of the medians) of triangle ABC. The endpoints of these medians are the midpoints of sides AB, BC< and CA. Once these three midpoints are connected, the medial triangle is formed (in red)

Orthic Triangle

The orthic triangle of a given triangle is constructed by connecting the feet of the three altitudes of the given triangle. Take a look at the following example:

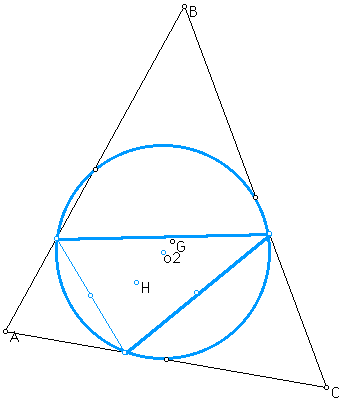
In this construction, point H is the orthocenter (intersection of the altitudes) of triangle ABC. The endpoints of these altitudes are constructed on sides AB,BC, and CA. Once these three points are connected, the orthic triangle is formed (in blue). The circumcircle of the orthic triangle can then be constructed (in blue). Point o2 is the center of this circle.

Orthocenter Mid-Segment Triangle

The orthocenter mid-segment triangle is constructed by connecting the midpoints of the three segments constructed by joining the orthocenter to each vertex of the original triangle. Take a look at the following example

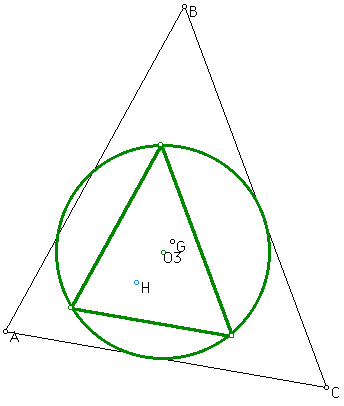
Note that H is the orthocenter of triangle ABC. The midpoints of segments HA, HB, and HC can be found. Once these midpoints are connected, the orthocenter mid-segment triangle can then be constructed (in green). The circumcircle of the orthocenter mid-segment triangle can then be constructed (in green). Point o3 is the center of this circle.

Now, Put Them All Together

Now take a look at the medial triangle, orthic triangle, and orthocenter mid-segment triangle all constructed together in triangle ABC

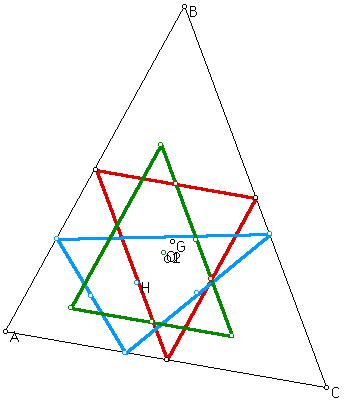
Then examine the circumcircle of these three triangles constructed together in triangle ABC

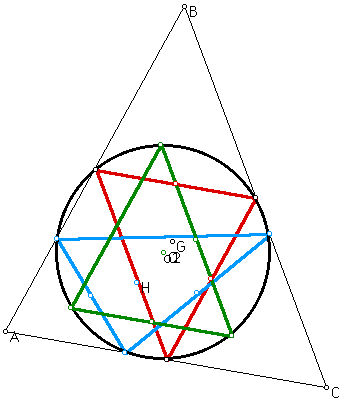
Hopefully, the reader notices that the three circumcircles seem to coincide (above, in black) Also o1,o2, and o3 from the three original circumcircles seem to come together to form a single point.

The Nine-Point Circle

So, this conjecture remains: given a triangle, the midpoints of the sides of the triangle, the feet of the altitudes of the triangle, and the midpoints of the segment from the vertices of the triangle to its orthocenter, there exists a unique circle that contains these nine points.

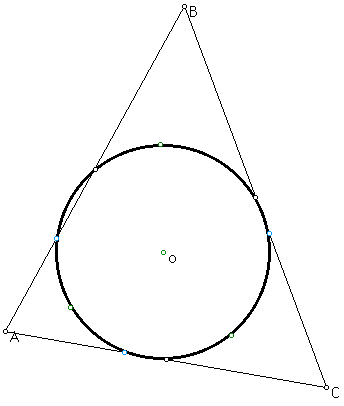
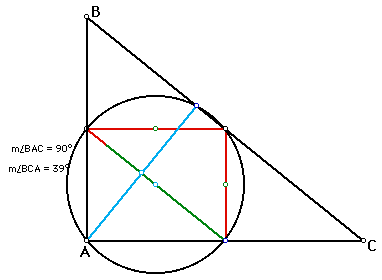
Hence the, this conjecture is true, and the circle is called the nine-point circle. It should be noted that the nine point circle exists when triangle ABC is a cute. For example take whenABC is right triangle, it can be noted that orthic triangle becomes aline connecting Point A and the foot of altitute of BC which make the two other end points of the orthic triangle to lie at the same point. On the other hand the medial triangle share the same segment as orthocenter and mid segment triangle as shown below. It appears that the points on the circle are only five given the other points happen to lie in the same point. That is to say for instance the two points of the median triangle and the orthocenter mid segment triangle happen to lie on the same point as shown below. One interesting aspect that I noted was that at the orthic triangle which is constructed by connecting the feet of the three altitudes, turned to be a single line since the two feets of the triangle ABC happen to lie on point 'A'and the other on segment BC.

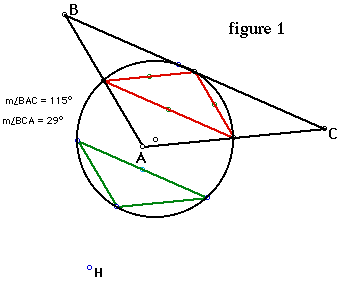
On the other hand when, when the triangle becomes abtuse, the orthic triangle dispear since the orthocenter is no longer inside the triangle ABC as shown in figure 1 below. For more demonstration, click here for more illustration.

Click here to see a proof by the author.