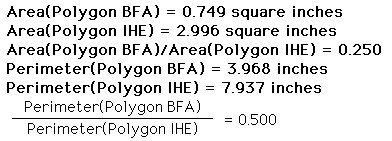"Biggie Size It"

Kim Seay

EMAT6680

In this exploration, I will look at the changes of the area and perimeter of various triangles when the length of the sides is doubled and tripled.
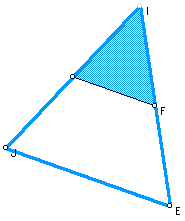
 I first start out with a triangle of any size. Then form another triangle that has sides twice as long as the first one.

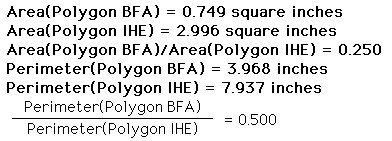
By forming a script, I can choose a triangle of any size (by choosing any three points) and another triangle with sides twice as long will automatically be created.

You can try this by clicking here to open a script in GSP. Open a new sketch, choose any three points and see what happens when you play the script.

By choosing different types of triangles, we can see that we appear to always be getting a pair of triangles with a ratio of .25 from the first to the second triangle, and a ratio of .5 for the perimeters.

What happens if we triple the length of the sides?

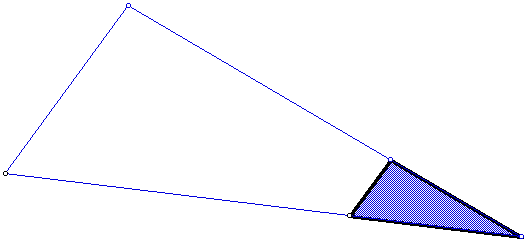Area(Polygon CFB) = 1.012 square inches
Perimeter(Polygon CFB) = 5.481 inches
Area(Polygon HGK) = 9.109 square inches
Perimeter(Polygon HGK) = 16.443 inches
Area(Polygon CFB)/Area(Polygon HGK) = 0.111
Perimeter(Polygon CFB)/Perimeter(Polygon HGK) = 0.333

You can try this yourself by clicking here and choosing any three points to create your first triangle. GSP will then use a script to create a second triangle with triple the length of each side.

As you can see, regardless of the points you choose, the pair of triangles seems to have a ratio of .111 for the area (from first to second triangle) and .333 for the ratio of the perimeters.

Conclusion:

I think this is an excellent exploration for students. It allows them to become familiar with GSP by determining the best way to "double" and "triple" the length of the sides. It is also an excellent way to introduce the scripts tool so students can try this out with several sets of triangles. This exploration also opens the door for many further investigations. As students begin to see a pattern emerge (the ratio between the perimeters is an obvious one), they will form new questions- "If I increased the lengths by five, will the ratio of the perimeters be .20?" This directly correlates with the NCTM's standard of students engaging in active problem solving.

Return