Exploring Areas
Kim Seay
EMAT 6680
To begin this problem, we
need a rectangle. Next, choose a point anywhere on one of the
sides of the rectangle. Form a triangle that has two shared vertices
and one shared side with the rectangle. Click
here for a GSP sketch that will allow you to choose any three
points and create a figure such as this.
The problem asks students
to compare the area of the triangle with that of the rectangle.
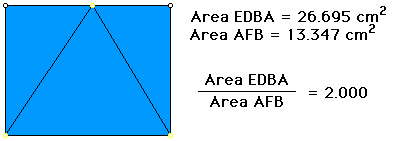In this case the area of
our triangle is half the area of the rectangle, or we could say
the ratio of areas from rectangle to triangle is 2:1. We can click
on point F at the top of the triangle and drag it along the side
of the rectangle to investigate if this will change the ratio
of the areas. Click here to try this.
As you can see, the ratio
will not change regardless of the location of point p. In fact,
this ratio will be the same given any rectangle and a triangle
that shares two of its vertices and one side. This makes sense
when we look at the formulas for finding the area.
Area of a rectangle
= length x height = l x h
Area of a triangle
= 1/2 base x height = 1/2bh
In this figure, height of
the rectangle and the triangle will always be the same. The base
of the triangle is the same as the length of the rectangle. To
find the area of the triangle, we simply take the area of the
rectangle and multiply by 1/2.
Conclusion:
I chose this application,
because it is very applicable to 6th grade math. This is a good
example of how GSP can be used in the middle school classroom.
Return